Please help!!

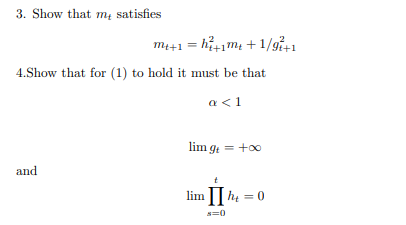
Consider the following model Pt = apit1 + Et Where pe is the endogenous variable (say an asset price), pry its expected value, and # an iid shock with zero mean and variance o', which is not known a period ahead. 1. What is the rational expectations equilibrium (REE)? Assume that instead of rational expectations, we have a learning process defined by Pit1 = Pit -(PI-1 - P; ). gt where of is a deterministic sequence of strictly positive numbers/ We will say that the learning process converges to the REE if lim E(Pit - Et,REEP +1)? = 0, where E is the unconditional expectations operator, and Et, REEP +1 is the value of pay in the rational expectations equilibrium, given the history of shocks. 2. Show that a necessary and sufficient condition for convergence to the REE is lim m; = 0. (1) 1-+ +00 where h2..h; + 8=1 95-13. Show that m, satisfies Mati=him+ 1/git1 4. Show that for (1) to hold it must be that lim of = too and lim IT he = 05. Show that the latter condition is asymptotically equivalent to 1/gt = too. 0 6. Does the learning process converge to the REE is g, is a constant? If 91 = 1/(t + 1)2? 7. Assume g: = 1/(t + 1). Show that (1) is satisfied (hint: use (2) and look for 8 > 0 such that one can show by induction that m,