please help

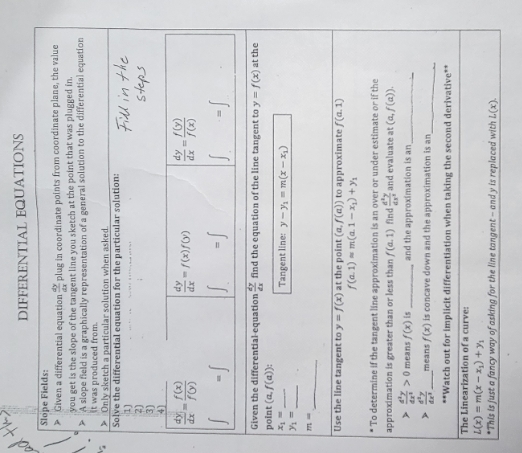
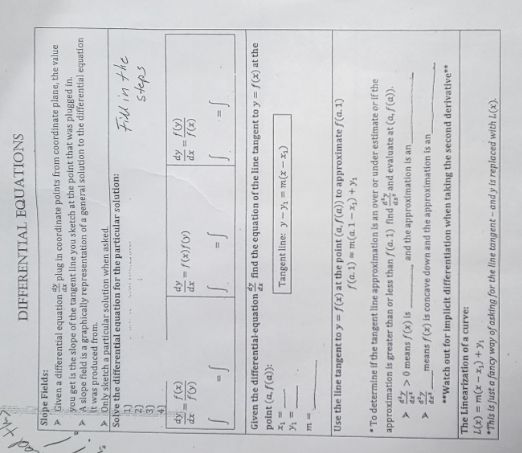
DIFFERENTIAL EQUATIONS Slope Fields: > Given a differential equation 1 plug in coordinate points from coordinate plane, the value you get is the slope of the tangent line you sketch at the point that was plugged in. A slope field is a graphically representation of a general solution to the differential equation it was produced from A Only sketch a particular solution when asked Solve the differential equation for the particular solution: Find in the steps dy f(x) dy dy _/0) dx /(x) Given the differential-equation - find the equation of the line tangent to y = /(x) at the point (a, /(a)): Tangent line: y- ym(x- x) Use the line tangent to y = /(x) at the point (a, /(a)) to approximate /(a. 1) F(al) = m(al-x) + ) " To determine If the tangent line approximation is an over or under estimate or if the approximation is greater than or less than / (a. 1) find s and evaluate at (a, /(a)). #2 0 means / (x) is and the approximation is an means / (x) is concave down and the approximation is an "Watch out for Implicit differentiation when taking the second derivative"* The Linearization of a curve: L(x) = m(x - 1) + 7 "This is just a fancy way of asking for the line tangent - and y is replaced with L(x)