please help!

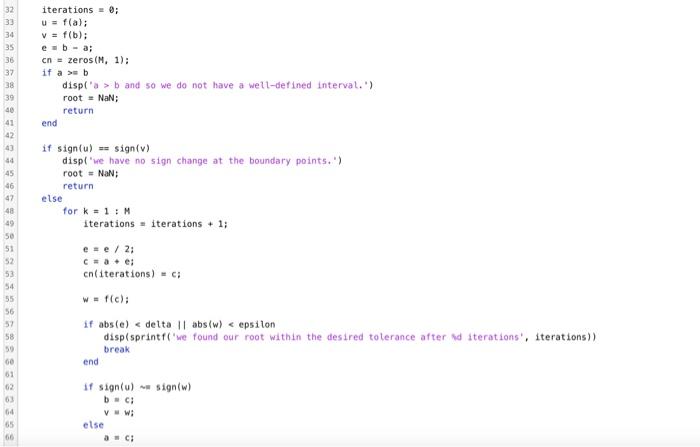
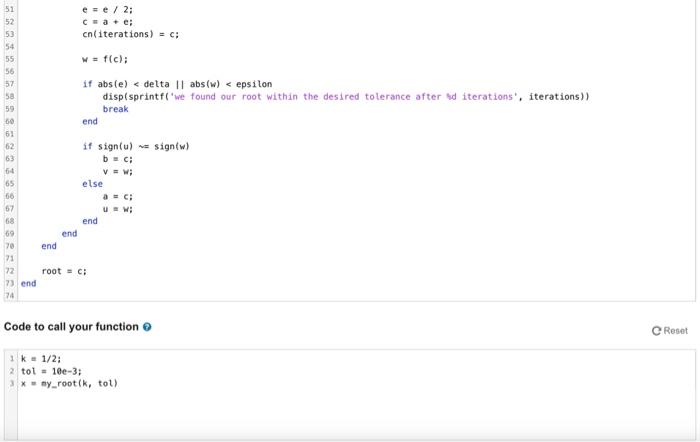
How Roots Vary With Respect to a Parameter. The function gc(x)=x2tan(x) has a root in the interval [1/5,1] whenever k[4,3/5]. Note: these are not necessary conditions on k. Write a function my_ root that computes this root of g1 using the provided bisection method code. Your function should accept the following inputs: - k=a number in [4,3/5], - tol = a posative parameter to control the size of gi Your fursction should return the following output: - x = computed root estimate of g4 found in the interval [1/5,1], such that g1(x)