Please Help me answer these questions

Thank you,

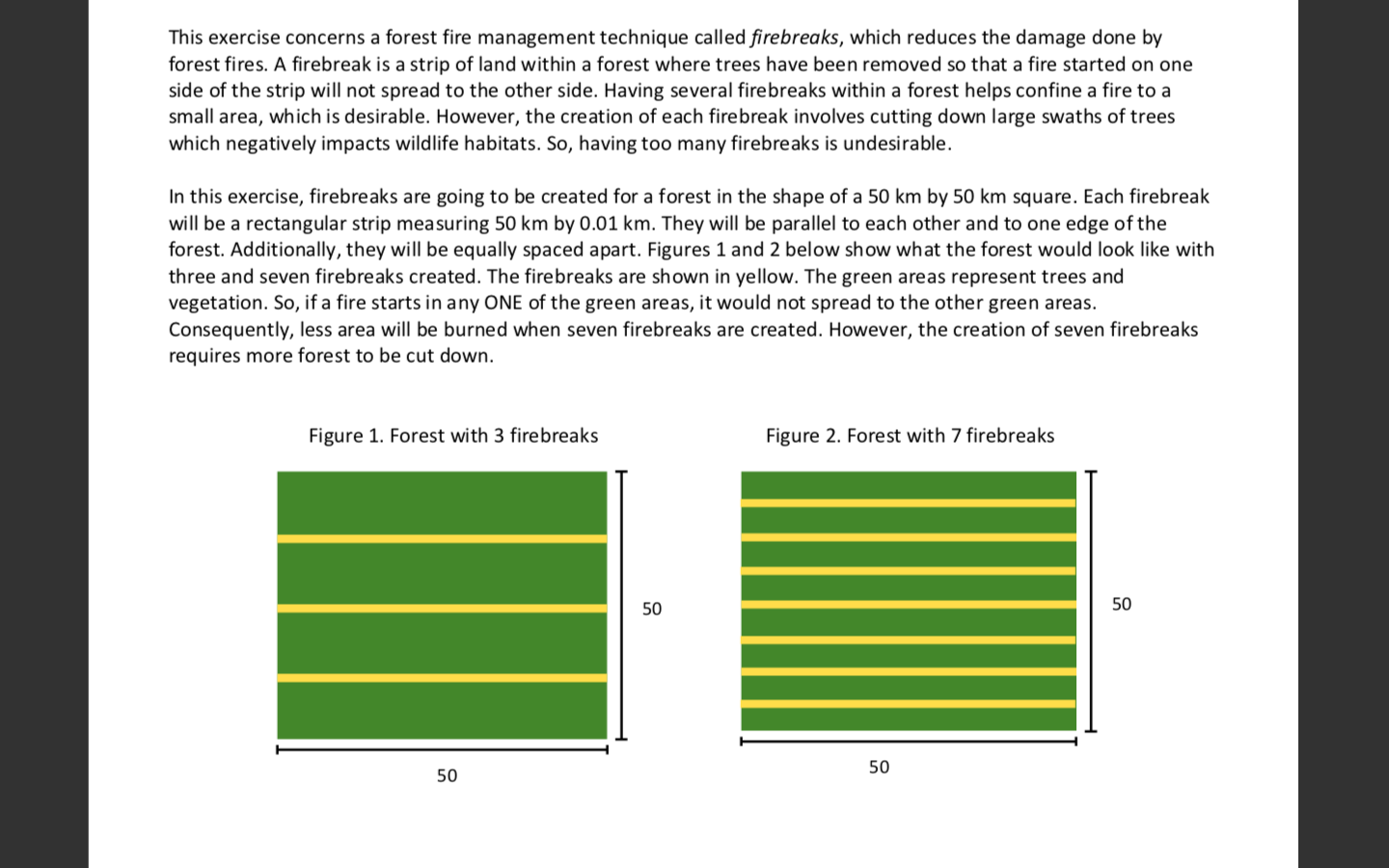
This exercise concerns a forest fire management technique called firebreaks, which reduces the damage done by forest fires. A firebreak is a strip of land within a forest where trees have been removed so that a fire started on one side of the strip will not spread to the other side. Having several firebreaks within a forest helps confine a fire to a small area, which is desirable. However, the creation of each firebreak involves cutting down large swaths of trees which negatively impacts wildlife habitats. So, having too many firebreaks is undesirable. In this exercise, firebreaks are going to be created for a forest in the shape of a 50 km by 50 km square. Each firebreak will be a rectangular strip measuring 50 km by 0.01 km. They will be parallel to each other and to one edge of the forest. Additionally, they will be equally spaced apart. Figures 1 and 2 below show what the forest would look like with three and seven firebreaks created. The firebreaks are shown in yellow. The green areas represent trees and vegetation. So, if a fire starts in any ONE of the green areas, it would not spread to the other green areas. Consequently, less area will be burned when seven firebreaks are created. However, the creation of seven firebreaks requires more forest to be cut down. Figure 1. Forest with 3 firebreaks Figure 2. Forest with 7 firebreaks 50 50 50 50 The objective of this exercise is to determine the optimal number of firebreaks to create for the above forest. The steps below will walk you through the process. a. Determine the area of the entire forest before any firebreaks were created. b. Determine the area of a single firebreak. C. Do some initial experimentation and calculations just to better understand the situation. Complete the table below. 3 firebreaks 90 firebreaks 4 Area cut down to create ALL firebreaks Remaining forested area Number of regions forest is divided into Area burned down from a fire started in one region of forest Total deforested area (burned area + all firebreaks) d. What do you learn from your calculations in part (c)? Discuss your observations. e. Let the function A(x) calculate the total deforested area when x firebreaks are created. If you calculated the table above correctly, should find that A(3) = 626.125 and A(90) = 71.978. If this isn't the case, you've made a mistake. Fix your mistake before you proceed! f. Complete the table below to determine a formula for A(x). x firebreaks Area cut down to create ALL firebreaks Remaining forested area Number of regions forest is divided into Area burned down from a fire started in one region of forest A(x) = Total deforested area (bumed area + all firebreaks) + g. Use your formula in part (f) to calculate A(90). You should again see that A(90) = 71.978. If this isn't the case, you've made a mistake in part (f). Fix your mistake before you proceed! h. Determine the ONE POSITIVE critical point of the function Ax) using the approach discussed in this course. You must show how you arrived at your answer. i. Use the first derivative test to determine if the critical point in part (h) is the location of a global maximum or a global minimum j. Calculate A(x) at the critical point. k. Draw a graph of the function Ax) by hand. Make sure you follow the instructions for drawing graphs! And, make sure the graph has the properties you determined in parts (h-j). I. Determine the optimal number of firebreaks to create for this forest and explain your reasoning. This exercise concerns a forest fire management technique called firebreaks, which reduces the damage done by forest fires. A firebreak is a strip of land within a forest where trees have been removed so that a fire started on one side of the strip will not spread to the other side. Having several firebreaks within a forest helps confine a fire to a small area, which is desirable. However, the creation of each firebreak involves cutting down large swaths of trees which negatively impacts wildlife habitats. So, having too many firebreaks is undesirable. In this exercise, firebreaks are going to be created for a forest in the shape of a 50 km by 50 km square. Each firebreak will be a rectangular strip measuring 50 km by 0.01 km. They will be parallel to each other and to one edge of the forest. Additionally, they will be equally spaced apart. Figures 1 and 2 below show what the forest would look like with three and seven firebreaks created. The firebreaks are shown in yellow. The green areas represent trees and vegetation. So, if a fire starts in any ONE of the green areas, it would not spread to the other green areas. Consequently, less area will be burned when seven firebreaks are created. However, the creation of seven firebreaks requires more forest to be cut down. Figure 1. Forest with 3 firebreaks Figure 2. Forest with 7 firebreaks 50 50 50 50 The objective of this exercise is to determine the optimal number of firebreaks to create for the above forest. The steps below will walk you through the process. a. Determine the area of the entire forest before any firebreaks were created. b. Determine the area of a single firebreak. C. Do some initial experimentation and calculations just to better understand the situation. Complete the table below. 3 firebreaks 90 firebreaks 4 Area cut down to create ALL firebreaks Remaining forested area Number of regions forest is divided into Area burned down from a fire started in one region of forest Total deforested area (burned area + all firebreaks) d. What do you learn from your calculations in part (c)? Discuss your observations. e. Let the function A(x) calculate the total deforested area when x firebreaks are created. If you calculated the table above correctly, should find that A(3) = 626.125 and A(90) = 71.978. If this isn't the case, you've made a mistake. Fix your mistake before you proceed! f. Complete the table below to determine a formula for A(x). x firebreaks Area cut down to create ALL firebreaks Remaining forested area Number of regions forest is divided into Area burned down from a fire started in one region of forest A(x) = Total deforested area (bumed area + all firebreaks) + g. Use your formula in part (f) to calculate A(90). You should again see that A(90) = 71.978. If this isn't the case, you've made a mistake in part (f). Fix your mistake before you proceed! h. Determine the ONE POSITIVE critical point of the function Ax) using the approach discussed in this course. You must show how you arrived at your answer. i. Use the first derivative test to determine if the critical point in part (h) is the location of a global maximum or a global minimum j. Calculate A(x) at the critical point. k. Draw a graph of the function Ax) by hand. Make sure you follow the instructions for drawing graphs! And, make sure the graph has the properties you determined in parts (h-j). I. Determine the optimal number of firebreaks to create for this forest and explain your reasoning