Question: Please help me! Please explain step by step and show work! THANK YOU FOR YOUR HEP! fffPre-Calculus/Trig 3 Name: UNIT 1: Algebra II Review -

Please help me! Please explain step by step and show work! THANK YOU FOR YOUR HEP!

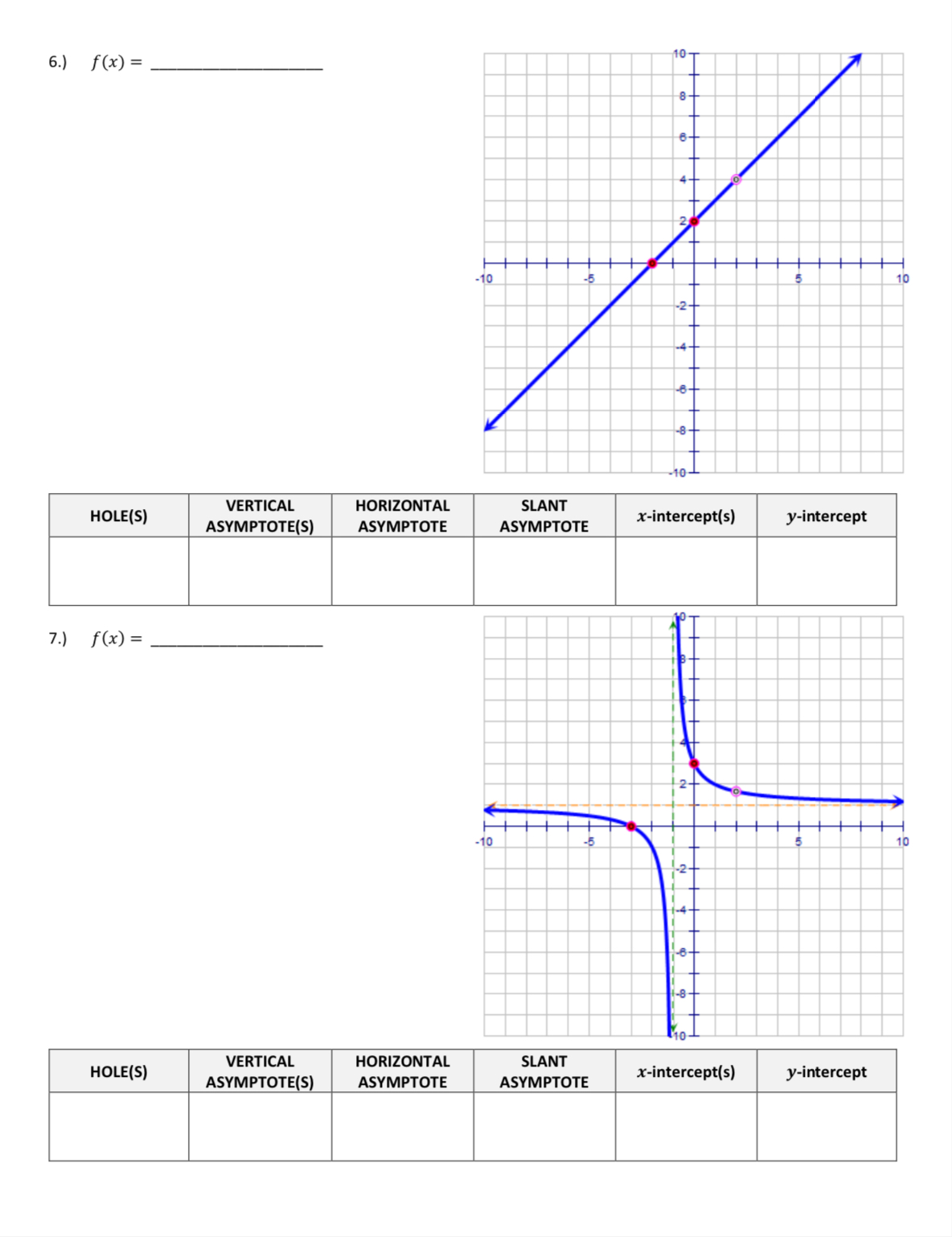
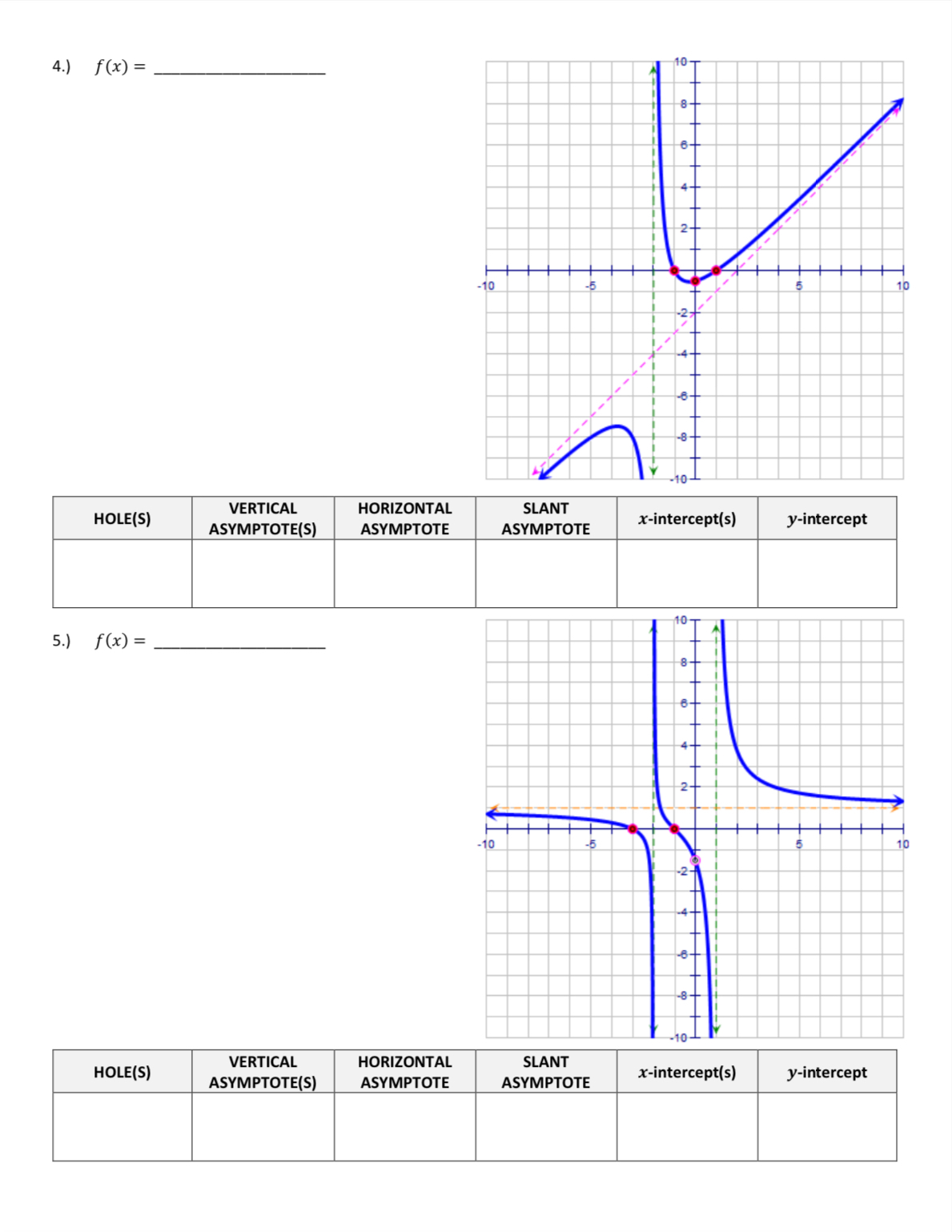
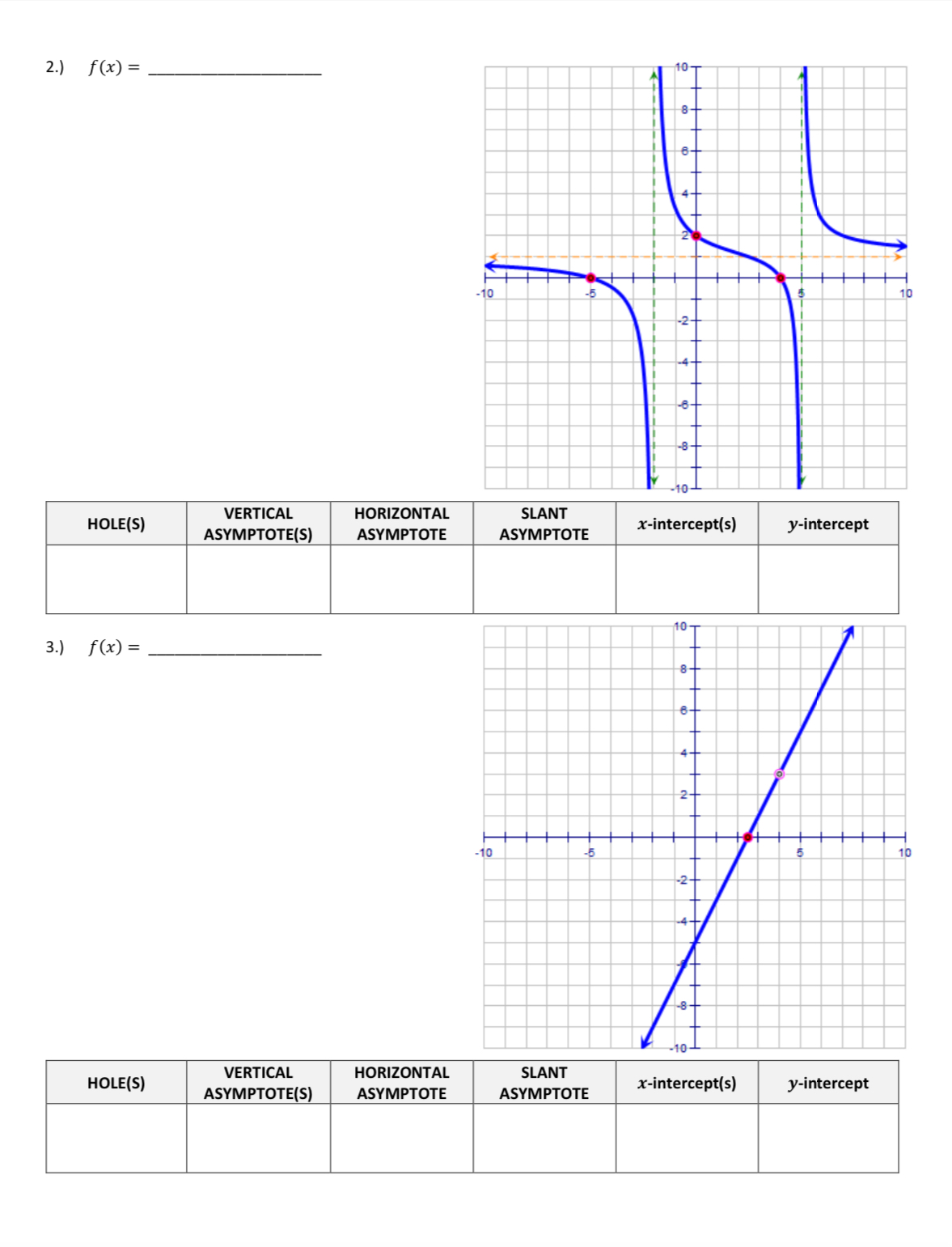
$YOU FOR YOUR HEP! \f\f\fPre-Calculus/Trig 3 Name: UNIT 1: Algebra II Review$ - SECTION 7 WORKSHEET #2 Date WRITING EQUATIONS OF RATIONAL FUNCTIONS To

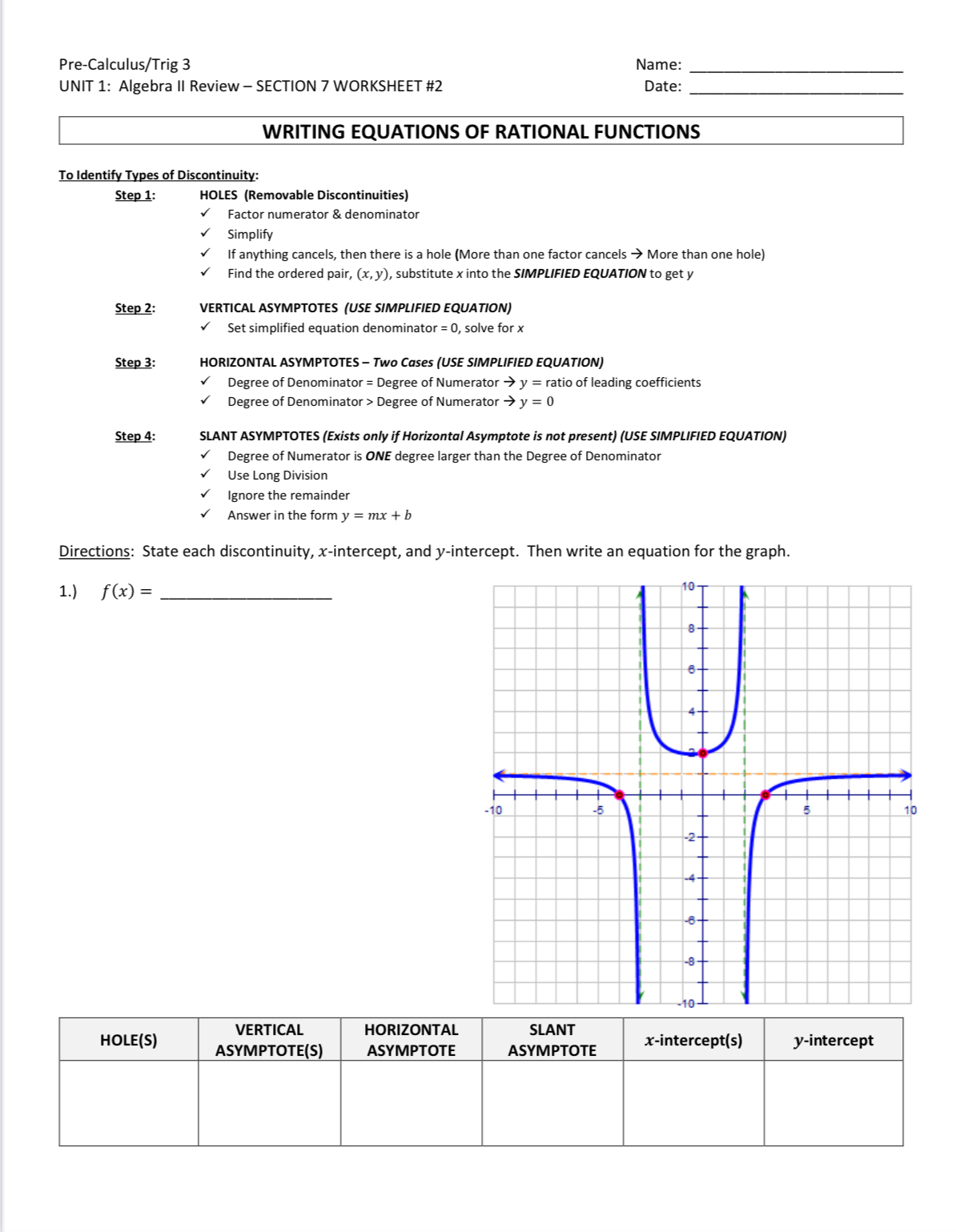
Identify Types of Discontinuity: Step 1: HOLES (Removable Discontinuities) Factor numerator &

\f\f\fPre-Calculus/Trig 3 Name: UNIT 1: Algebra II Review - SECTION 7 WORKSHEET #2 Date WRITING EQUATIONS OF RATIONAL FUNCTIONS To Identify Types of Discontinuity: Step 1: HOLES (Removable Discontinuities) Factor numerator & denominator Simplify If anything cancels, then there is a hole (More than one factor cancels > More than one hole) Find the ordered pair, (x, y), substitute x into the SIMPLIFIED EQUATION to get y Step 2: VERTICAL ASYMPTOTES (USE SIMPLIFIED EQUATION) Set simplified equation denominator = 0, solve for x Step 3: HORIZONTAL ASYMPTOTES - Two Cases (USE SIMPLIFIED EQUATION) Degree of Denominator = Degree of Numerator > y = ratio of leading coefficients Degree of Denominator > Degree of Numerator > y = 0 Step 4: SLANT ASYMPTOTES (Exists only if Horizontal Asymptote is not present) (USE SIMPLIFIED EQUATION) V Degree of Numerator is ONE degree larger than the Degree of Denominator Use Long Division Ignore the remainder Answer in the form y = mx + b Directions: State each discontinuity, x-intercept, and y-intercept. Then write an equation for the graph. 1 . ) f (x ) = U 10 HOLE(S) VERTICAL HORIZONTAL SLANT ASYMPTOTE(S) ASYMPTOTE ASYMPTOTE x-intercept(s) y-intercept

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

I am doing tax return project. attachments are the materials professor provide. He wants me to do a current year engagement file (Similar with prior year engagement file). AC 371 Tax Return Project...

I am so lost with all of this and the worst part it is due in an hour and a half. I don't know what to do please help. In this course you will have the opportunity to apply the concepts learned to a...

London School of Science & Technology Qualification Unit number and title BTEC Level 5 HND Diploma Business UNIT 6: Business Decision Making Student name and ID number Assessor name Al Hassan Barrie...

MBA 5652, Research Methods Course Syllabus Course Description Business research methods will guide students in advancing their knowledge of different research principles and their applicability in...

Please attemp the question I have attached and I have guideline for the answers.For question 3,difference between tax evasion and avoiddance can be found in seminar 2 slides.Tax avoidance mean the...

UNIT 5 QZ, Q-20 UNIT 5 / UNIT 8 QUESTIONS KEEP ANSWERS SEPARATE BY UNITS UNIT II STUDY GUIDE Consumer Mathematics Reading Assignment See information below. Key Terms 1. Add-on interest method 2....

Math 012 Final Examination Answer Sheet Fall 2016 1 Math 012 Intermediate Algebra Name______________________________ Final Examination: Fall 2016 Instructor __________________________ Answer Sheet...

please help me to find the answer for part 1, part3 and part4 Queensland University of Technology QUT Business School School of Accountancy AYB 339 Accountancy Capstone Integrated Case Study Semester...

uestion: 1. IN A STOCK ACQUISITION ACCOUNTED FOR BY THE EQUITY METHOD, A PORTION OF THE PURCHASE PRICE OFTEN IS ATTRIBUTABLE TO GOODWILL OR TO SPECIFIC ASSETS OR LIABILITIES. HOW OR UNDER WHAT BASIS...

On November 17 of Year 1, the company entered into a commitment to purchase 250,000 ounces of gold on February 14 of Year 2 at a price of $310.20 per ounce. On December 31 of Year 1, the market price...

5. Hall generators are normally used to measure a) impulse voltages b) unidirectional impulse currents c) any type of impulse currents d) large ac currents

Using Excel in Financial Modeling: Group of answer choices To track investments performance over time For probability models and trend analyses to predict performance and risk To Create more...

2023 1040 form 1.Phillip and Claire are married and file a joint return. Phillip is self-employed as a real estate agent, and Claire is a flight attendant. Phillip and Claire have three dependent...