Question: Please help me! Problem 1: Recall from the lecture notes that the (Cartesian) product of two sets A, B, written A B, is the set
Please help me!
Problem 1: Recall from the lecture notes that the (Cartesian) product of two sets A, B, written A B, is the set {(a, b)| a ? A, b ? B}, i.e. the set of all ordered pairs with first entry in A and second in B. Determine which of the following are true and which are false; if they are true provide a proof, if false give a counterexample.
- If A B = B A implies A = B.
I did it 2 ways and both comments said it needed to be edited.
1st way:
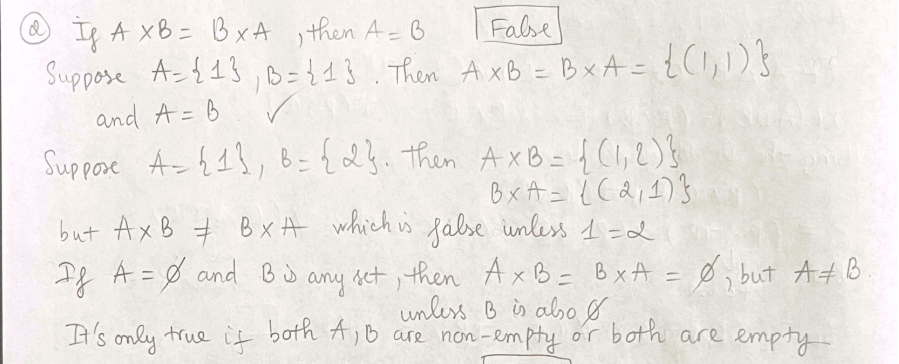
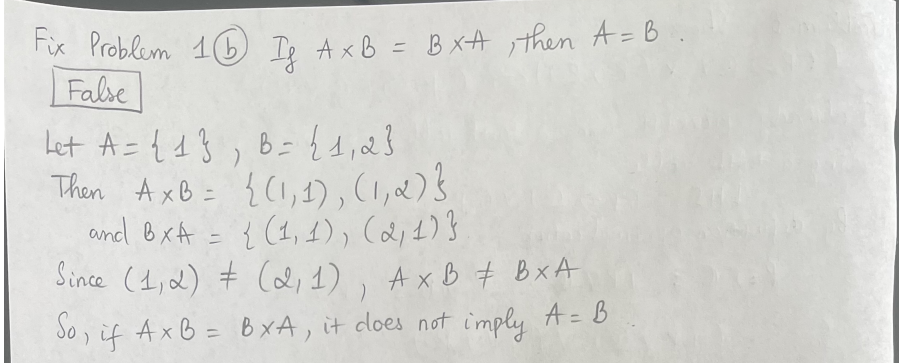
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


