please help me solve and explain along the way! Thank you!!

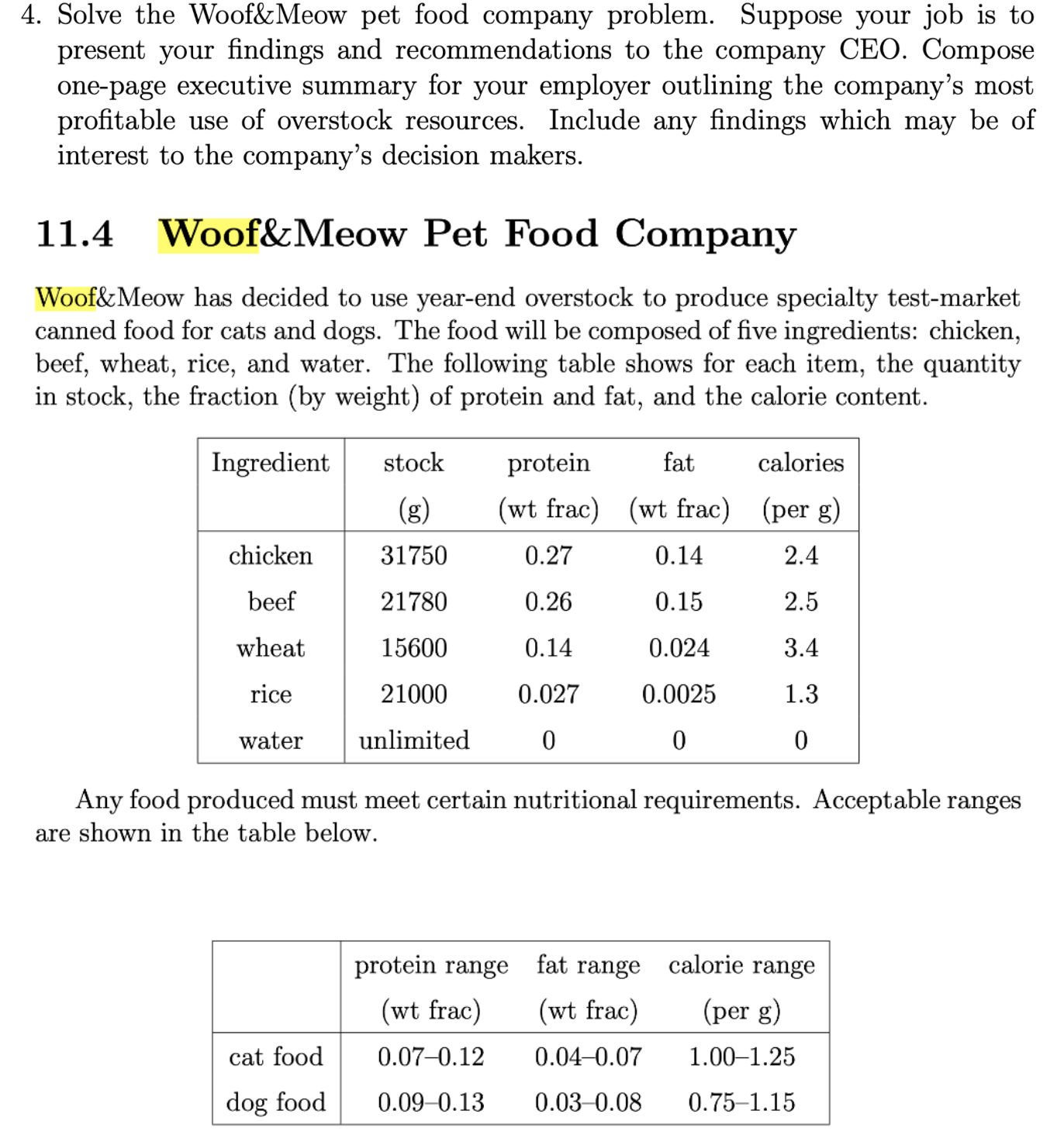
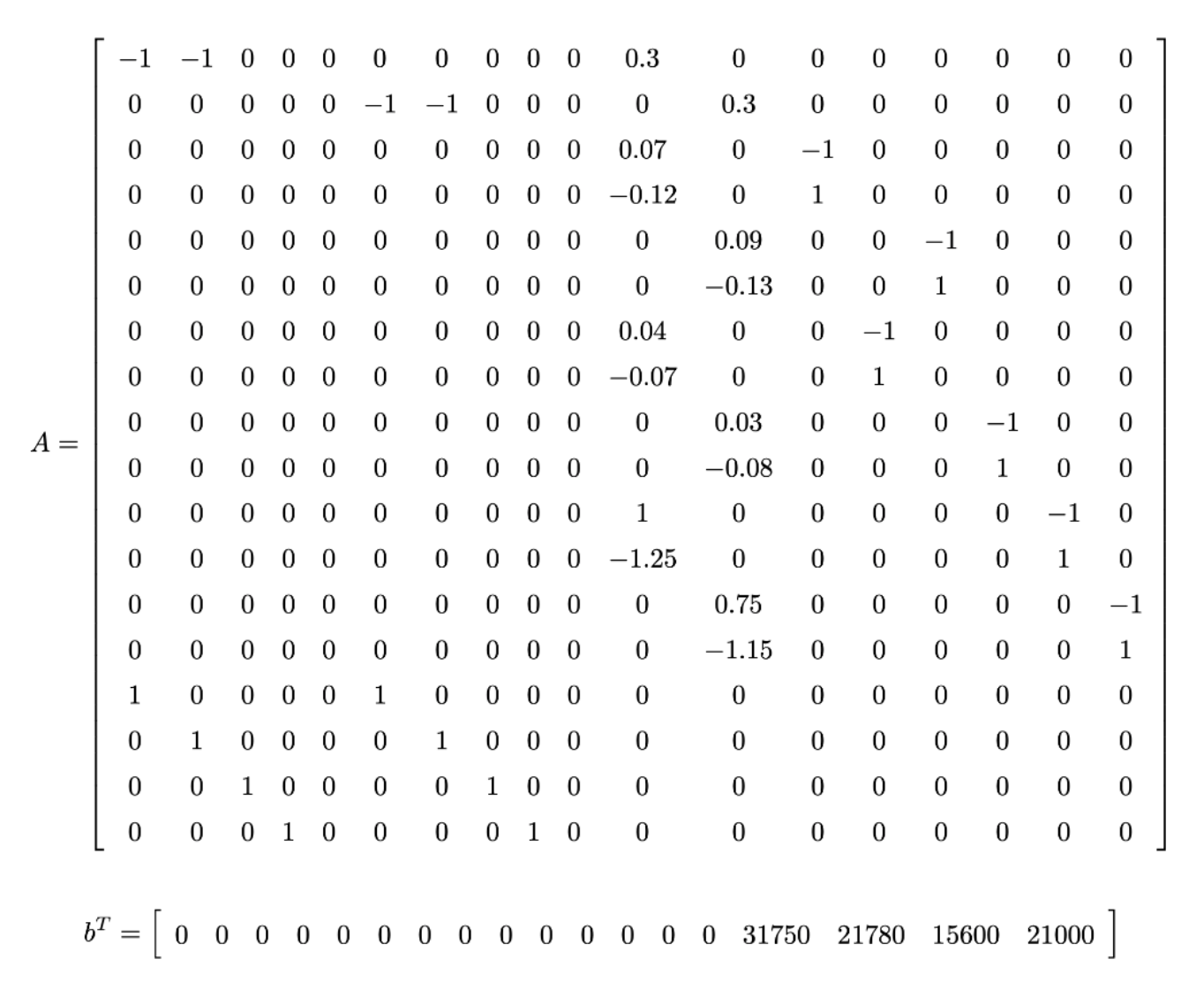
4. Solve the Woof&Meow pet food company problem. Suppose your job is to present your ndings and recommendations to the company CEO. Compose one-page executive summary for your employer outlining the company's most protable use of overstock resources. Include any ndings which may be of interest to the company's decision makers. 11.4 Woof&Meow Pet Food Company Woof&Meow has decided to use year-end overstock to produce specialty test-market canned food for cats and dogs. The food Will be composed of ve ingredients: chicken, beef, wheat, rice, and water. The following table shows for each item, the quantity in stock, the fraction (by weight) of protein and fat, and the calorie content. Ingredient stock protein fat calories (a) (wt fraC) (W's I5mm) (per a) 31750 0.27 0.14 2.4 21780 0.26 0.15 2.5 15600 0.14 0.024 3.4 21000 0.027 0.0025 1.3 unlimited 0 0 0 Any food produced must meet certain nutritional requirements. Acceptable ranges are shown in the table below. protein range fat range calorie range (wt frac) (wt frac) (per g) cat food 0.070.12 0.040.07 1.001.25 dog food 0.090.13 0.030.08 0.751.15 In addition, consumer appreciation and marketability requirement suggest that any food produced must contain at least 30% meat by weight. Formulate a linear program whose solution provides a recipe for a batch of dog food and a batch of cat food that maximizes the total weight of overstock used in the process. Solution. We must determine how much of each ingredient is used in each type of food. Let xi,- = the grams of ingredient 1' used in food 3', where i = 1, 2, 3, 4, 5 corresponds to chicken, beef, wheat, rice and water, respectively; and j = 1,2 corresponds to cat food and dog food, respectively. We can consider 1353' 6 1R. Because there are many constraints on various relative quantities, we will also use the following dependent variables. W;- = the total weight of food 3'. Wm = the total protein weight in food 3'. ij = the total fat weight in food j. C, = the total calories in food 3'. All together there are 18 decision variables. The objective is to maximize the use of overstock ingredients (by weight). That is, we seek to maximize the objective function z = $11 + .1321 + $31 + $41 + $12 + $22 + $32 + 3342. We begin enumerating the problem constraints by dening our dependent variables in terms of our initial decision variables. W1 = $11 + $21 +3331 + $41 + 1'51- W2 = $12 + $22 + 3332 + $42 + 1'52- WP] = 0.27:1:11 + 0.26321 + 0.14:1:31 + 0.0273641. Wfl = 0.1451311 + 0.159321 + 0.0243231 + 0.0025x41. ng = 0.273312 -| 0.263922 + 0.143332 + 0.0275642. ng = 0.143312 + 0.15.7522 + 0.0245332 + 0002511742. 01 = 2.42311 + 2.51221 + 3.411131 + 1.33341. 02 = 2.42212 + 2.55822 -|- 3.4.1332 + 1.3:842. Now, our inequality constraints are relatively simply expressed in terms of our augmented set of decision variables. For example, the requirement that cat food be at least 30% meat by weight is expressed as $11 + 3721 W 2 0.3 or equivalently $11 1321 + 0.3W1 5 0. 1 Notice that the above equivalence assumes that W1 > 0. For this particular problem we can be reasonably assured that this will be the case at the optimal solution. That is, we expect Wf > 0. However, the denominator of any such constraint should be checked once the problem is solved to make sure that the equivalency is met. The corresponding constraint for dog food is $12 + $22 W 2 0.3 01' equivalently 3512 $22 + 0.3W2 S 0. 2 There are constraints on the weight fraction of protiens. For the cat food we have W 1 0.07 0 for any feasible 3;. For dog food we have the corresponding constraints 0.09W2 - Wp2 _ 0 and - 0.13W2 + Wp2 5 0. We also have similar constraints on the weight fraction of fats: 0.04W1 - W/1 5 0 and - 0.07W1 + W/1 0. 0.03W2 - W/2