please help me solve problem 1 and problem 2

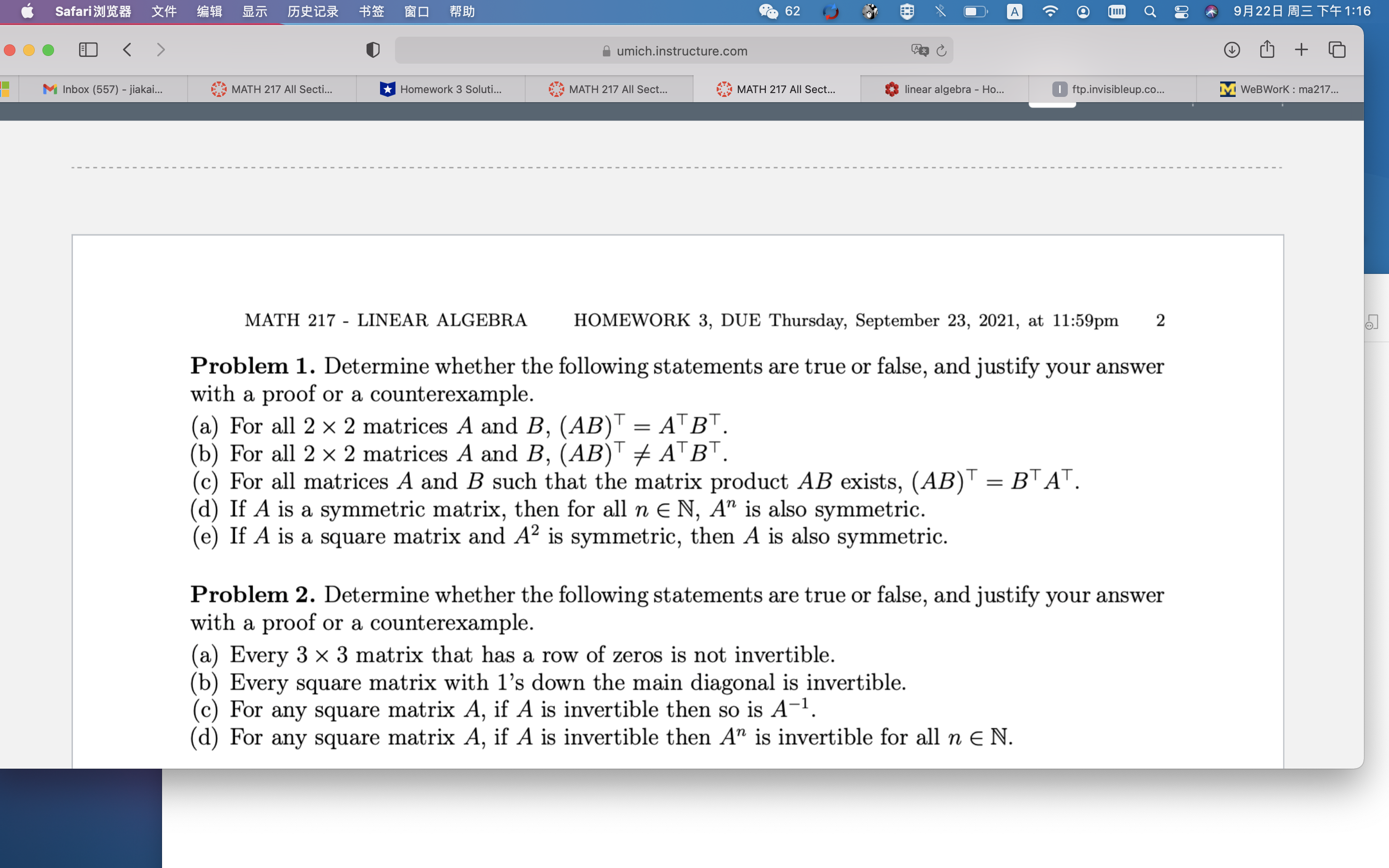
6 wt ' \\" \" {r . i , ezzaEETFme MATH 217 - LINEAR ALGEBRA HOMEWORK 3, DUE Thursday, September 23, 2021, at 11:59pm 2 5 Problem 1. Determine whether the following statements are true or false, and justify your answer with a proof or a counterexample. (a) For all 2 x 2 matrices A and B, (AB)T = ATBT. (b) For all 2 x 2 matrices A and B, (AB)T 7E ATBT. (c) For all matrices A and B such that the matrix product AB exists, (AB)T = BTAT. (d) If A is a symmetric matrix, then for all n e N, A" is also symmetric. (e) If A is a square matrix and A2 is symmetric, then A is also symmetric. Problem 2. Determine whether the following statements are true or false, and justify your answer with a proof or a counterexample. (a) Every 3 x 3 matrix that has a row of zeros is not invertible. (b) Every square matrix with 1's down the main diagonal is invertible. (c) For any square matrix A, if A is invertible then so is A'l. (d) For any square matrix A, if A is invertible then A" is invertible for all n E N