please help me solve these

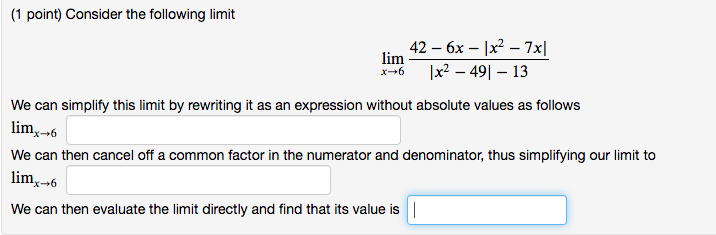
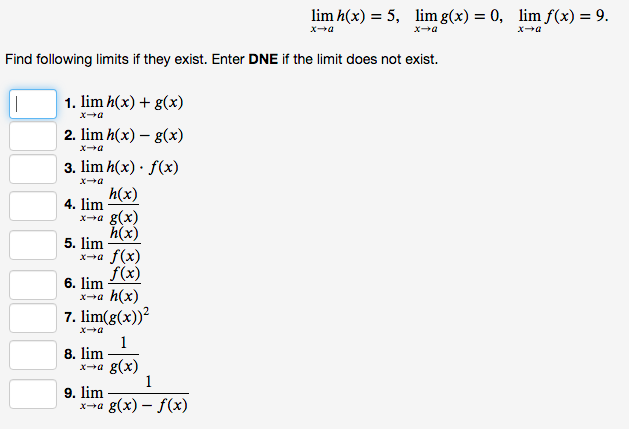
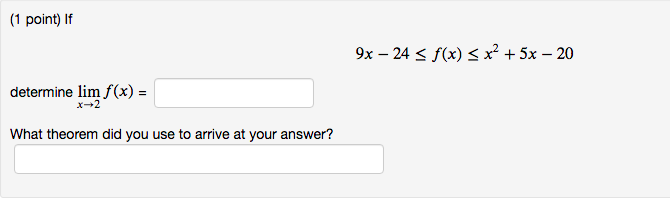
(1 point) Consider the following limit lim 42 - 6x - |x2 - 7x| x-6 |x2 - 491 - 13 We can simplify this limit by rewriting it as an expression without absolute values as follows lim -6 We can then cancel off a common factor in the numerator and denominator, thus simplifying our limit to lim, -6 We can then evaluate the limit directly and find that its value islim h(x) = 5, limg(x) =0, lim f(x) = 9. x-+0 Find following limits if they exist. Enter DNE if the limit does not exist. 1. lim h(x) + g(x) 2. lim h(x) - g(x) 3. lim h(x) . f(x) 4. lim h(x) no g(X) 5. lim h(x) f(x) 6. lim f(x) ka h(x) 7. lim(g(x))2 8. lim 1=0 g(X) 9. lim x-a g(x) - f(x)(1 point) If 9x - 24