Please help me solve this problem in MatLab software?

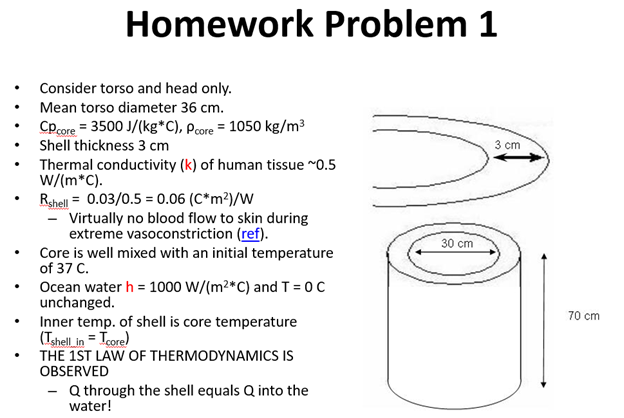
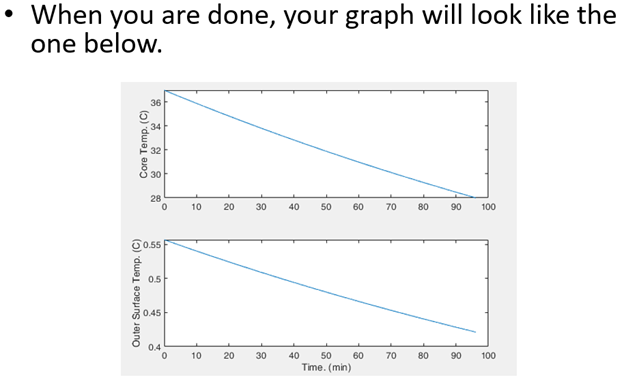
Homework Problem 1 in 3 cm Consider torso and head only. Mean torso diameter 36 cm. CP.core = 3500 J/(kg*C), Pcore = 1050 kg/m3 Shell thickness 3 cm Thermal conductivity (k) of human tissue ~0.5 W/(m*C). Rshell = 0.03/0.5 = 0.06 (C*m2)/W Virtually no blood flow to skin during extreme vasoconstriction (ref). Core is well mixed with an initial temperature of 37 C. Ocean water h = 1000 W/(m2*C) and T = 0 C unchanged. Inner temp. of shell is core temperature (Tshell in = Tcore) THE 1ST LAW OF THERMODYNAMICS IS OBSERVED Q through the shell equals Q into the water! 30 cm 70 cm Here is all but 6 lines of the program! The "while" replaces the familiar "for" here, allowing the operation to be stopped when thermal death is reached (28 C). clear, clc h = 1000; W/(m2*C) Onet = 100; u TW = 0; 8C Tcore (1) - 37; C Cp - 3500; * J/(kg*c) r = 1050; kg/m3 R = 0.06; (m2*C)/W Dcore = 0.30; core diameter, m Dos - 0.36; $os - "outer shell", m ht -.7; Vcore - (pi*Dcore 2/4) *ht; 3 dt = 1; + 3 Aos - pi*Dos*ht; m2 lis - pi*Dcore"ht; m 2 Aavg - (Aos + Ais)/2; m2 Tos (1) - 1; * 1st guess, C t(1) - 1; s i = 1; while Tcore (1) >- 28 1 - 1 + 1; end subplot (2,1,1), plot (t/60, Tcore) ylabel('Core Temp. (C)') subplot (2,1,2), plot (t/60, Tos) xlabel('Time (min)') ylabel(' Outer Surface Temp. (C)') . In the instructions, it says that you must observe the first law of thermodynamics. What does that mean? The rate of heat transfer through the outer shell is Aavg* (Tcore - Tos)/R. - where R is the thermal resistance of the outer shell. The rate of heat transfer from the surface of the body into the water is Ags *(Tos - TW)/(1/h) - where (1/h) is the thermal resistance at the convective surface. By the first law, these two values must be equal (Q reaching the surface must equal Q being carried away). This means that Aave* (Tcore - Tos)/R = Aos*(Tos - Tw)/(1/h) or, re-written: Aavg. * (Tcore - Tos)/R - Aos * (Tos - Tw)/(1/h) = 0 * OS In the above equation, we know everything except the outer surface temperature that makes Q through the shell equal to Q from the shell to the water. You could do the algebra to rewrite this equation to find Tos: Tos(i-1) =(Aavg*Tcore(i1)+Aos*Tw*h* Rshell)/(Aavg+Aos*h*Rshell) What comes out is the equation that will allow you, during each step of your simulation, to find the outer surface temperature that satisfies the 1st law. Notice the Qmet term in the model. The victim is still alive during the period in the water. This means that metabolic heat is being produced (100 W is a bit above basal metabolic heat production). This heat actually prolongs the cooling period in the model. Remove this term and notice what happens to the cooling time. dT = (Qmet -Q)/(r*Cp*Vcore) It is possible to argue using both physiology and engineering that the Amet term shouldn't be included. How would you argue that?. When you are done, your graph will look like the one below. 36 Core Temp. (C) 30 28 0 10 20 30 40 50 60 70 80 90 100 0.55 0.5 Outer Surface Temp. (C) 0.45 0.4 0 10 20 30 70 80 90 100 40 50 60 Time. (min) Homework Problem 1 in 3 cm Consider torso and head only. Mean torso diameter 36 cm. CP.core = 3500 J/(kg*C), Pcore = 1050 kg/m3 Shell thickness 3 cm Thermal conductivity (k) of human tissue ~0.5 W/(m*C). Rshell = 0.03/0.5 = 0.06 (C*m2)/W Virtually no blood flow to skin during extreme vasoconstriction (ref). Core is well mixed with an initial temperature of 37 C. Ocean water h = 1000 W/(m2*C) and T = 0 C unchanged. Inner temp. of shell is core temperature (Tshell in = Tcore) THE 1ST LAW OF THERMODYNAMICS IS OBSERVED Q through the shell equals Q into the water! 30 cm 70 cm Here is all but 6 lines of the program! The "while" replaces the familiar "for" here, allowing the operation to be stopped when thermal death is reached (28 C). clear, clc h = 1000; W/(m2*C) Onet = 100; u TW = 0; 8C Tcore (1) - 37; C Cp - 3500; * J/(kg*c) r = 1050; kg/m3 R = 0.06; (m2*C)/W Dcore = 0.30; core diameter, m Dos - 0.36; $os - "outer shell", m ht -.7; Vcore - (pi*Dcore 2/4) *ht; 3 dt = 1; + 3 Aos - pi*Dos*ht; m2 lis - pi*Dcore"ht; m 2 Aavg - (Aos + Ais)/2; m2 Tos (1) - 1; * 1st guess, C t(1) - 1; s i = 1; while Tcore (1) >- 28 1 - 1 + 1; end subplot (2,1,1), plot (t/60, Tcore) ylabel('Core Temp. (C)') subplot (2,1,2), plot (t/60, Tos) xlabel('Time (min)') ylabel(' Outer Surface Temp. (C)') . In the instructions, it says that you must observe the first law of thermodynamics. What does that mean? The rate of heat transfer through the outer shell is Aavg* (Tcore - Tos)/R. - where R is the thermal resistance of the outer shell. The rate of heat transfer from the surface of the body into the water is Ags *(Tos - TW)/(1/h) - where (1/h) is the thermal resistance at the convective surface. By the first law, these two values must be equal (Q reaching the surface must equal Q being carried away). This means that Aave* (Tcore - Tos)/R = Aos*(Tos - Tw)/(1/h) or, re-written: Aavg. * (Tcore - Tos)/R - Aos * (Tos - Tw)/(1/h) = 0 * OS In the above equation, we know everything except the outer surface temperature that makes Q through the shell equal to Q from the shell to the water. You could do the algebra to rewrite this equation to find Tos: Tos(i-1) =(Aavg*Tcore(i1)+Aos*Tw*h* Rshell)/(Aavg+Aos*h*Rshell) What comes out is the equation that will allow you, during each step of your simulation, to find the outer surface temperature that satisfies the 1st law. Notice the Qmet term in the model. The victim is still alive during the period in the water. This means that metabolic heat is being produced (100 W is a bit above basal metabolic heat production). This heat actually prolongs the cooling period in the model. Remove this term and notice what happens to the cooling time. dT = (Qmet -Q)/(r*Cp*Vcore) It is possible to argue using both physiology and engineering that the Amet term shouldn't be included. How would you argue that?. When you are done, your graph will look like the one below. 36 Core Temp. (C) 30 28 0 10 20 30 40 50 60 70 80 90 100 0.55 0.5 Outer Surface Temp. (C) 0.45 0.4 0 10 20 30 70 80 90 100 40 50 60 Time. (min)