Please help me to check my answer. If my answer has error, please correct it to me, thank you.

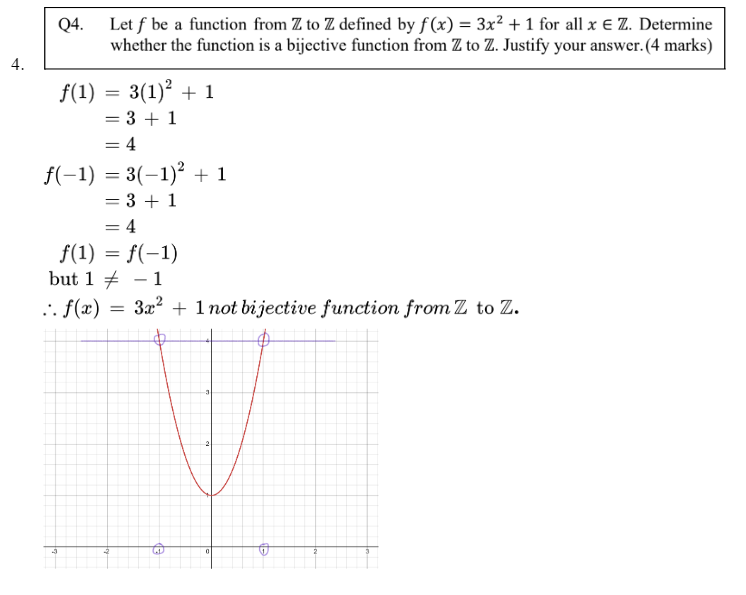
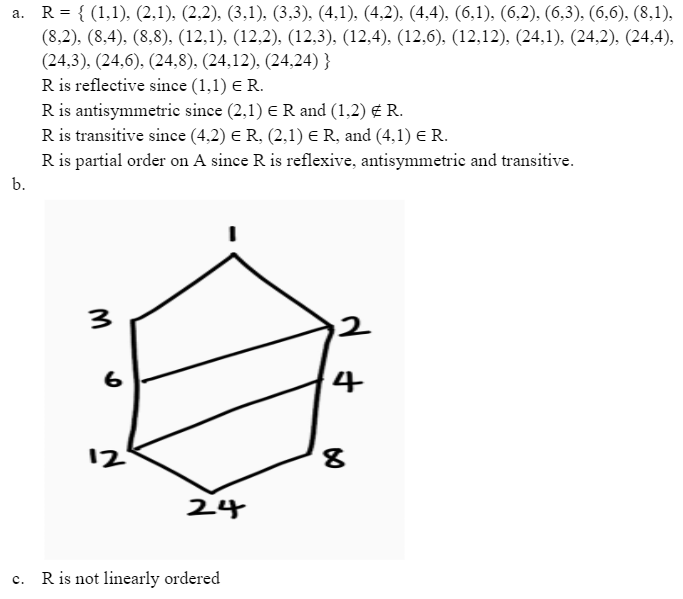
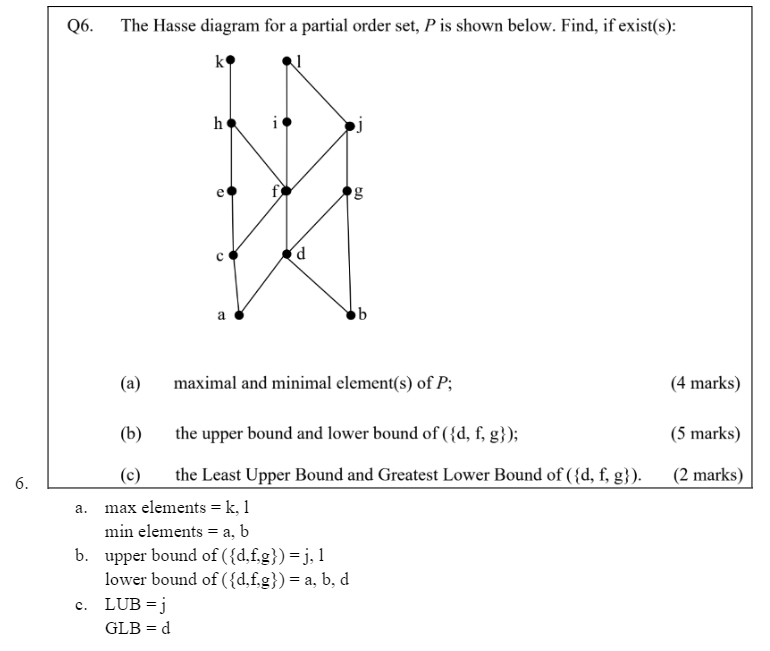
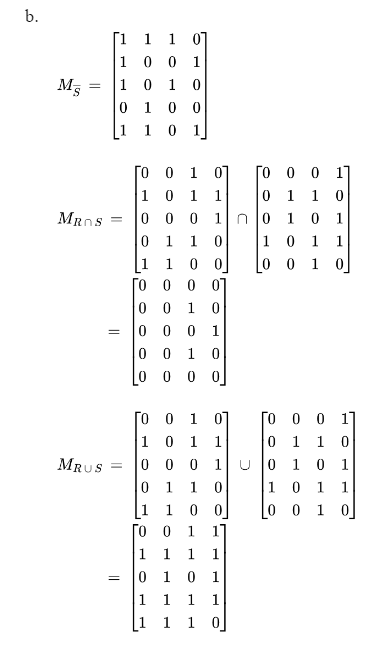
Q1. Let A = {1,2,3,4,5], B = {1,2,3,4), and R = {(1,3), (2,1), (2,3), (2,4), (3,4), (4,2), (4,3), (5,1), (5,2)], S = {(1,4), (2,2), (2,3), (3,2), (3,4), (4,1), (4,3), (4,4), (5,3)}, be relations from A to B. (a) Find MR and MS. (2 marks) (b) Compute Ms, MRnS, MRUS, MR-1, MR-1.5. (5 marks) 1.a. 0 01 0 101 1 MR = 0 0 01 01 1 0 1 1 0 (0 0 0 17 01 10 Ms 01 0 1 101 1 0 010\f1o Let A = {1,2,3,4,5} and let R be a relation on A represented by 0 0 Find the matrix representation for the reflexive closure of R. (2 marks) Find the matrix representation for the symmetric closure of R. (2 marks) Find the matrix representation for the transitive closure of R by using Warshall's algorithm. (6 marks) Reflexive closure of R. = { (1,1), (1,3), (2,1), (2,2), (2,3), (3,2), (3,3), (3,4), (3,5), (4,3). (4,4), (4.5). (5,1), (5,2), (5,5) } 1 0 10 0 1 1 10 0 01 1 1 1 0 01 1 1 MRref = 1 0 0 1 b. Symmetric closure of R = R U R.1 R. = { (1,3), (2,1), (2,3), (3,2), (3,4), (3,5), (4,3), (4,4), (4,5), (5,1), (5,2) } R.1 = { (3,1), (1,2). (3,2), (2,3), (4,3), (5,3), (3,4), (4,4), (5,4), (1,5), (2,5) } 0 1 1 0 1] 10101 1 101 1 0 01 1 1 MRURI= 1 1 1 10\fQ3. Let A = {1,2,3,4,5,6,7} and 4 P1 = INy 3 P2 = A WN WH O W NA NOIN aAWAD P3 = (a) Compute pi, pz and (p; . pz!) . p3. (6 marks) (b) Write P1, P2 and p3 as product of disjoint cycles. Hence determine whether each of the permutations is even or odd. (3 marks) 3.\fQ4. Let f be a function from Z to Z defined by f (x) = 3x2 + 1 for all x E Z. Determine whether the function is a bijective function from Z to Z. Justify your answer. (4 marks) f(1) = 3(1)~ + 1 =3 +1 = 4 f(-1) = 3(-1) +1 =3 +1 = 4 f(1) = f(-1) but 1 * - 1 .. f(x) = 3x' + 1 not bijective function from Z to Z. 2Let A = {1,2,3,4,6,8,12,24} and R be the relation on 4 defined by xRy if and only if x 1s a multiple of y. (a) Is R a partial order on A? Justify your answer. (4 marks) Draw the Hasse diagram of the relation R on A, or explain why the Hasse diagram does not exist. (4 marks) Is R linearly ordered? (1 mark) . R. = { (1,1), (2,1), (2,2), (3,1), (3,3), (4,1), (4,2), (4,4), (6,1), (6,2), (6,3), (6,6), (8,1), (8,2). (8,4), (8,8), (12,1), (12,2), (12,3), (12,4), (12,6), (12,12), (24,1), (24,2), (24.4), (24,3), (24,6), (24,8), (24,12), (24,24) } R is reflective since (1,1) E R. R. is antisymmetric since (2,1) e R and (1,2) # R. R is transitive since (4.2) E R, (2,1) e R, and (4,1) E R. R. is partial order on A since R is reflexive, antisymmetric and transitive. b. 3 6 12 8 24 c. R is not linearly orderedQ6. The Hasse diagram for a partial order set, P is shown below. Find, if exist(s): k I (a) maximal and minimal element(s) of P; (b) the upper bound and lower bound of ({d, f, g}); (c) the Least Upper Bound and Greatest Lower Bound of ({d, f, g}). a. max elements=k. 1 min elements = a. b b. upper bound of ({d.f.g})=.1 lower bound of ({d.f.g})=a.b.d c. LUB=j GLB=d (4 marks) (5 marks) (2 marks)