Please Help Me understand how to write the extended euclidian algorithm in python with 4 returned values

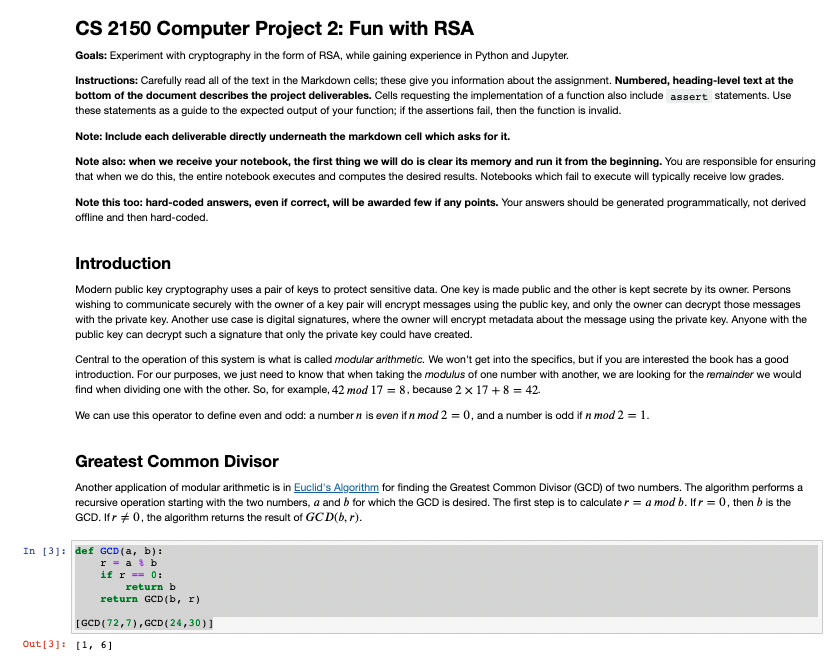
CS 2150 Computer Project 2: Fun with RSA Goals: Experiment with cryptography in the form of RSA, while gaining experience in Python and Jupyter. Instructions: Carefully read all of the text in the Markdown cells; these give you information about the assignment. Numbered, heading-level text at the bottom of the document describes the project deliverables. Cells requesting the implementation of a function also include assert statements. Use these statements as a guide to the expected output of your function; if the assertions fail, then the function is invalid. Note: Include each deliverable directly underneath the markdown cell which asks for it. Note also: when we receive your notebook, the first thing we will do is clear its memory and run it from the beginning. You are responsible for ensuring that when we do this, the entire notebook executes and computes the desired results. Notebooks which fail to execute will typically receive low grades. Note this too: hard-coded answers, even if correct, will be awarded few if any points. Your answers should be generated programmatically, not derived offline and then hard-coded. Introduction Modern public key cryptography uses a pair of keys to protect sensitive data. One key is made public and the other is kept secrete by its owner. Persons wishing to communicate securely with the owner of a key pair will encrypt messages using the public key, and only the owner can decrypt those messages with the private key. Another use case is digital signatures, where the owner will encrypt metadata about the message using the private key. Anyone with the public key can decrypt such a signature that only the private key could have created. Central to the operation of this system is what is called modular arithmetic. We won't get into the specifics, but if you are interested the book has a good introduction. For our purposes, we just need to know that when taking the modulus of one number with another, we are looking for the remainder we would find when dividing one with the other. So, for example, 42 mod 17 = 8, because 2 x 17 + 8 = 42 We can use this operator to define even and odd: a number n is even if n mod 2 = 0, and a number is odd if n mod 2 = 1. Greatest Common Divisor Another application of modular arithmetic is in Euclid's Algorithm for finding the Greatest Common Divisor (GCD) of two numbers. The algorithm performs a recursive operation starting with the two numbers, a and b for which the GCD is desired. The first step is to calculate r = a mod b.lfr = 0, then b is the GCD. Ifr #0, the algorithm returns the result of GCD(b,r). In [3]: def GCD(a, b): r = a b if r -- 0: return b return GCD(b, r) [GCD (72,7), GCD( 24,30) Out[3] : [1, 61 Extended Euclidean Algorithm There is another version of Euclid's algorithm known as the Extended Euclidean algorithm which keeps track of the quotient of alb as well as two additional integers and t of Bzout's identity, which we will put to good use later. In the Extended Euclidean Algorithm, we keep track of three sequences of numbers defined as follows: ro= a 1 = b r = r,-2-917-1 So = 1 $1 = 0 = :-2-419-1 to = 0 11=1 ; = 1-2-911-1 As in the earlier algorithm, the extended algorithm works recursively until it finds some ri = 0 at which point it is done. First, we check the modulus of a and b.lfr is not 0, we proceed to finding the current value of q which is the integer quotient of a and b. We then use to find the next values of sandt. We then repeat the process until we encounter anr = 0. Example 1: EGCD(30,24) t 9 0 30 1 0 1 24 0 1 2 6 1 -11 3 0 Example 2: EGCD(72,7) S t 9 0 72 1 0 1 7 0 1 2 2 2 1 -10 10 3 1 3 31 3 40 At this point, wherer, = 0, then r;-1 is the GCD, and we'll have a keen interest in the values in that row. In (): Deliverable #1: A function implementing the Extended Euclidean Algorithm The function should take arguments a and b an return the values of r:-1,8-1,*-1, and 4-1 where r; = 0. Two assertions are provided to check your work In [8]; import math def eged(a,b): # TODO: implement Extended Euclidean Algorithm and return the values r, s, t, and g from the row *before* r = 0 return [r, s, t,9) assert eged (72,7) == [1,-3, 31,3] assert egcd (24,30) == [6, -1, 1, 1] AssertionError Traceback (most recent call last) in 10 return r, s, t,q] 11 ---> 12 assert egcd (72,7) == [1,-3, 31,3] 13 assert eged(24,30) == [6, -1, 1, 1] AssertionError: Why all this extra work? Well, Bzout's identity can be given by the equation: as; +ht; = GCD(a, b) where j = 1 - 1, which will come in handy in a few moments