Question: Please help me with the second image, number 3 below. Thank you! Theorem 5.8. Consider a power series f(z) = Can(z - zo). 1. If

Please help me with the second image, number 3 below. Thank you!

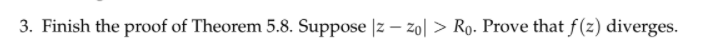
Theorem 5.8. Consider a power series f(z) = Can(z - zo)". 1. If f converges at a point z1 / Zo, then it is absolutely convergent at Z . Ro every point z satisfying |z - zo| Ro. Proof. 1. By the nith term test, the sequence (an (Z1 - Zo)" ) converges (to 0) and is therefore bounded by some MER+. Thus [am| |z - zo|" = [an| |21 - zol" z - ZO Ro. Prove that f (z) diverges

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

1 2.3 Definition of a Discrete Probability Function Definition: Let S be a discrete sample space from some experiment. A function P, defined on all events in S, is said to be a probability function...

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

MATHEMATICIANS RISE TO A CHALLENGE ne of the theorems we teach in eighth grade is a + b= *, where c is the length of the hypotenuse of a right triangle in Euclidean space, and a and b are the lengths...

Please help me make an Executive Summary. Explain what you will examine in the case study. Write an overview of the field you are researching. Make a thesis statement and sum up the results of your...

A financial services company monitors loan applications. Every day 50 applications are assessed for the accuracy of the information on the form. Results for 20 days are where Di is the number of...

Here's a plot showing the federal rate on 3-month Treasury bills from 1950 to 1980, and a regression model fit to the relationship between the Rate (in %) and Years Since 1950. a) What is the...

In a q , the complement of the output of the last flipflop is connected back to the D input of the first flip - flop

Problem 2-3 Compute the multifactor productivity measure for each of the weeks shown for production of chocolate bars. Assume 40-hour weeks and an hourly wage of $16. Overhead is 1.5 times weekly...

2. In this chapter, the reader should reflect on the following concepts : Thomas theorem, premise of action, utterance and mental constructions.

11. Based on the following rules regarding the confidence we have in information in a communication context, find examples from your everyday life where the rules have relevance: (a) The spatial rule...

2. Describe a situation from your own everyday life where it is clear that the situation in its consequence becomes the way you define it.