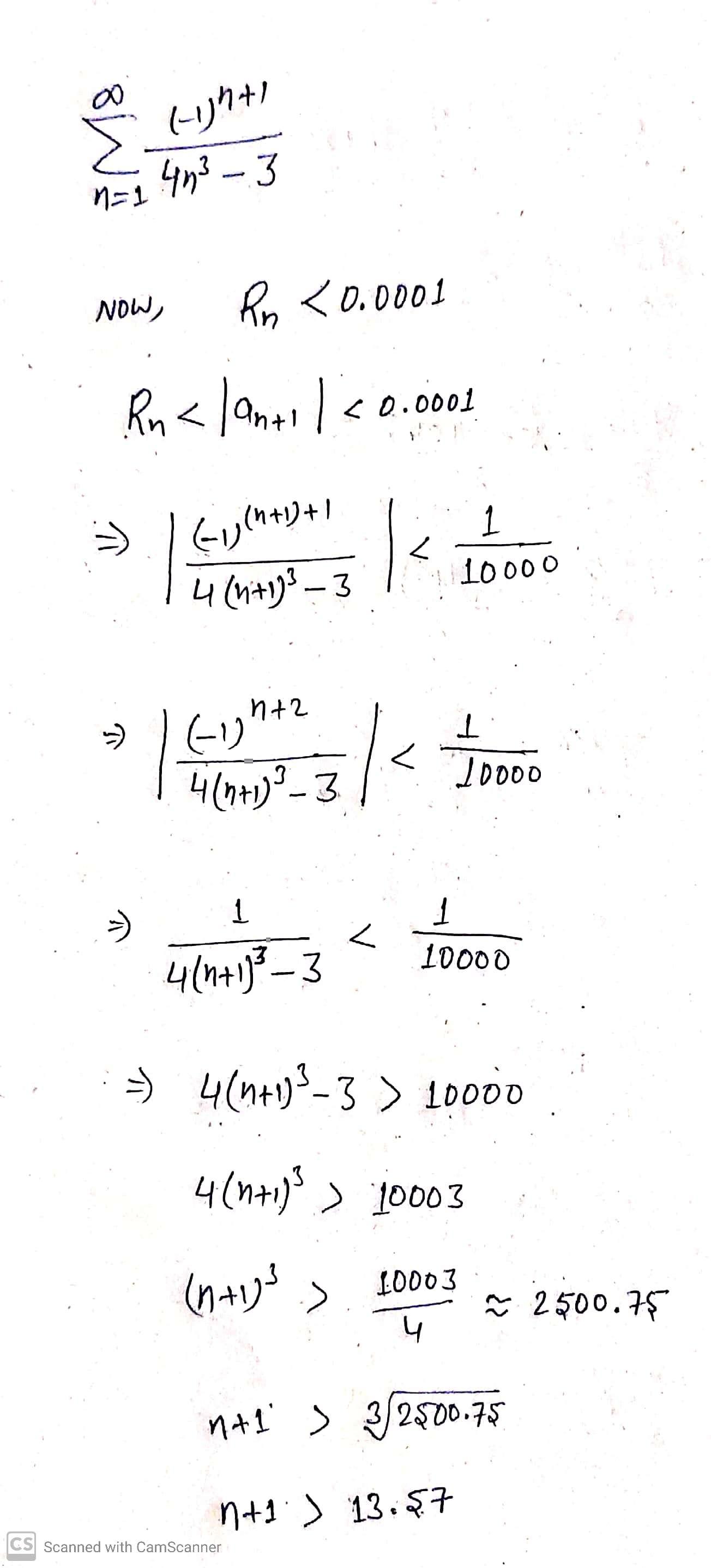
Please help me with these three questions

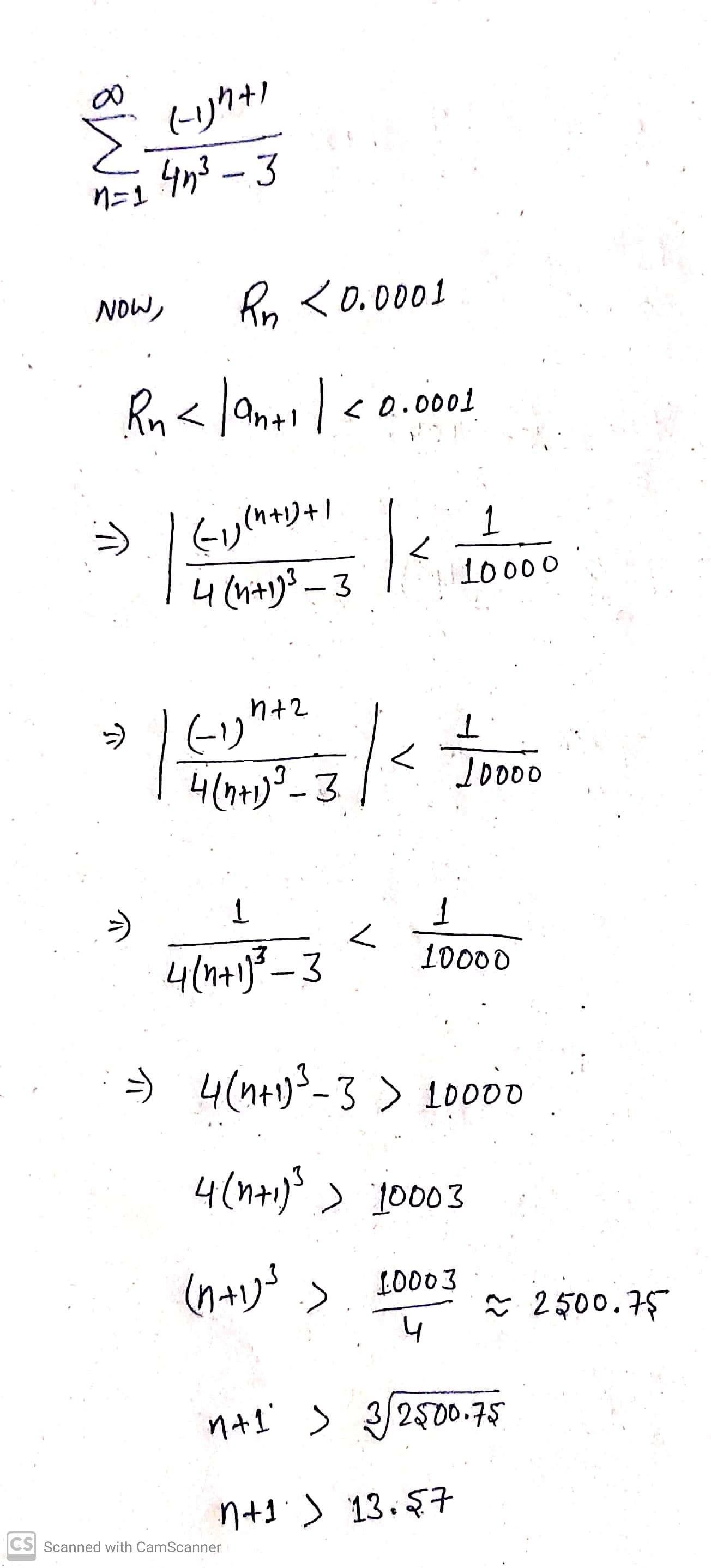
Use the Alternating Series Remainder Theorem to determine the smallest number of terms required to approximate the sum of the series with an error of less than 0.0001. (-1)7+1 n = 1 9n3 - 8 XDetermine the smallest degree of the Maclaurin polynomial required for the error in the approximation of the function at the indicated value of x to be less than 0.001. f(x) = e , approximate f(-0.15)Use the definition of Taylor series to find the first four nonzero terms of the Taylor series, centered at c, for the function. g(x) = i 1 + x, C = 0 900 = (-ijh+1 M8 1 = 1 403 - 3 NOW , Rn 10003 10003 4 2 2500.75 n+ 1 ) 3 /2500.75 n+ 1 ) 13.57 CS Scanned with CamScannern > 12. 57 213 h >13 so, the smallest number of teams is 13 CS$canned with CamScanner