Please help me with this problem. Thank you

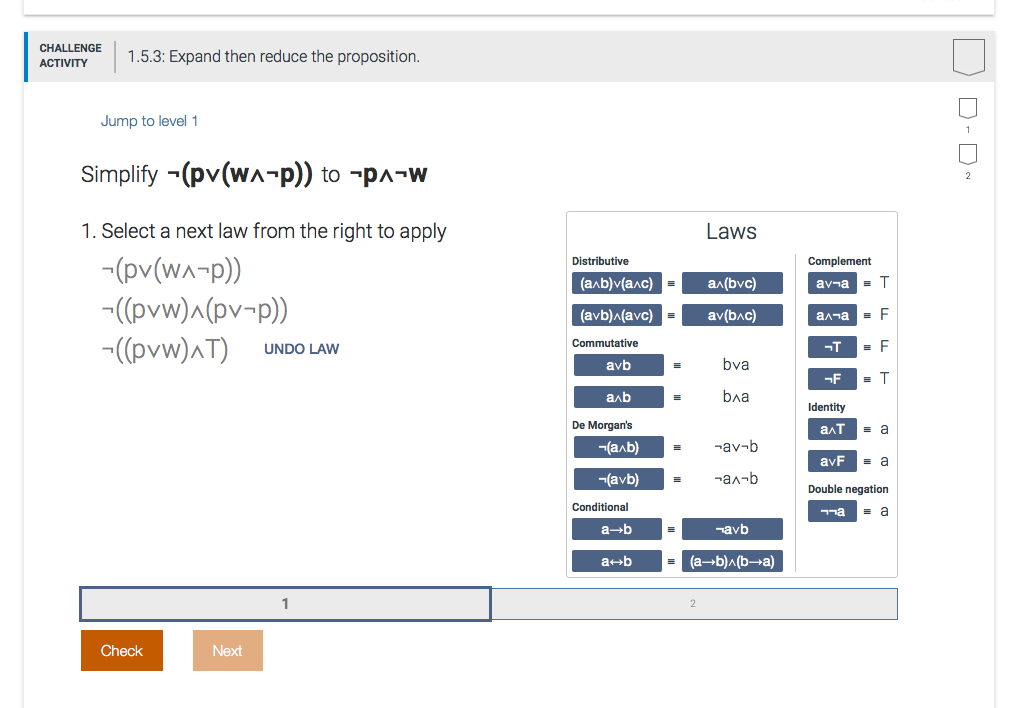
CHALLENGE ACTIVITY 1.5.3: Expand then reduce the proposition. Jump to level 1 Simplify -(pv(wa-p)) to -Pa-W Laws Distributive Complement avna 1. Select a next law from the right to apply -(pv(wa-p)) -((pvw)^(pv-p)) -(pvw)AT) (a b)(a c) = an(bvc) (avb) (avc) = av(bac) = F UNDO LAW Commutative -T EF avb bva F T aab baa Identity De Morgan's (axb) -av-b avF = a (avb) -a-b Double negation Conditional a Ea ab Tavb ab (a+b)^(-a) Check Next