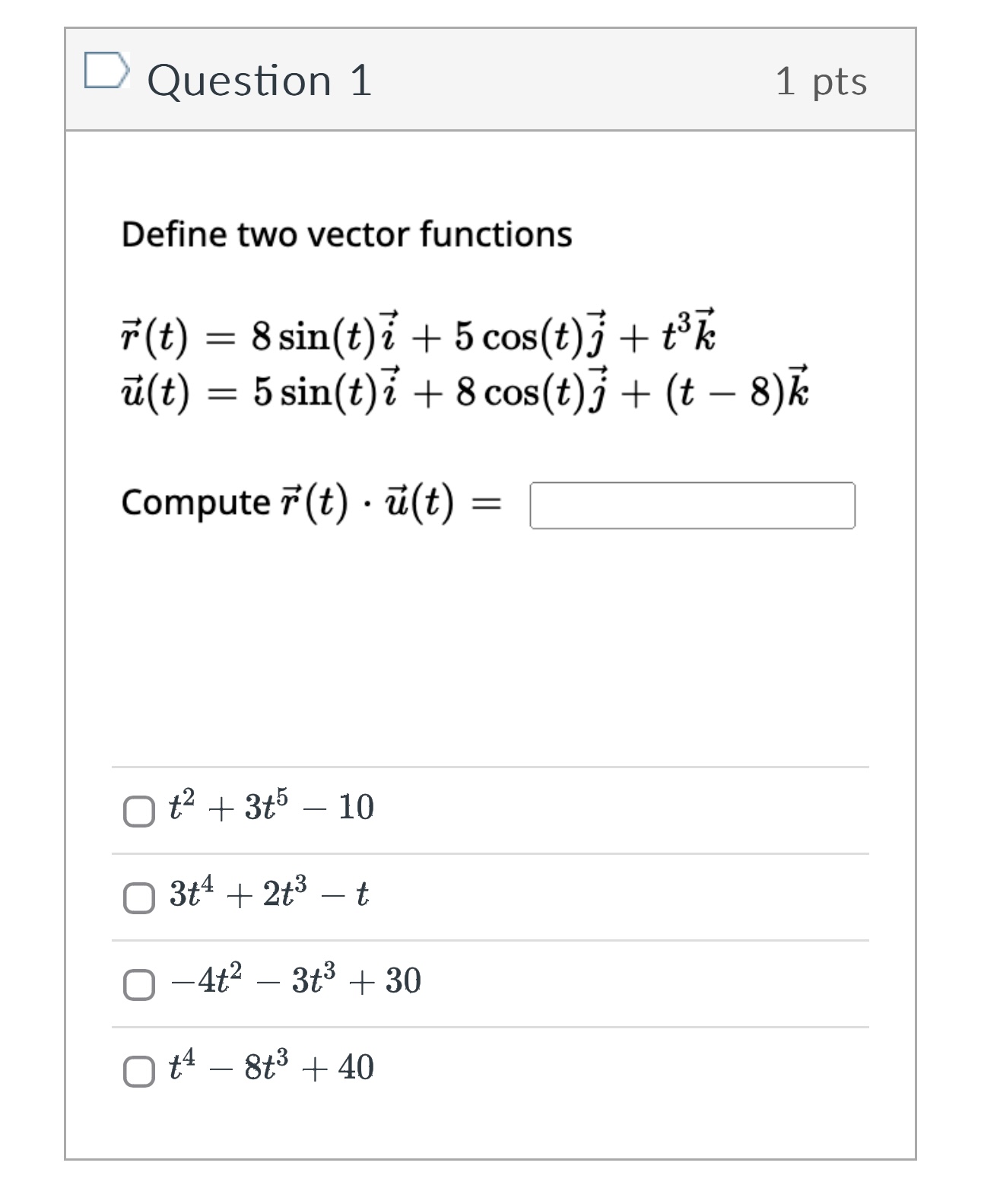
Question: Please help me with this question as soon as possible. Thank you so much! Question 1 1 pts Define two vector functions T (t) =
Please help me with this question as soon as possible. Thank you so much!
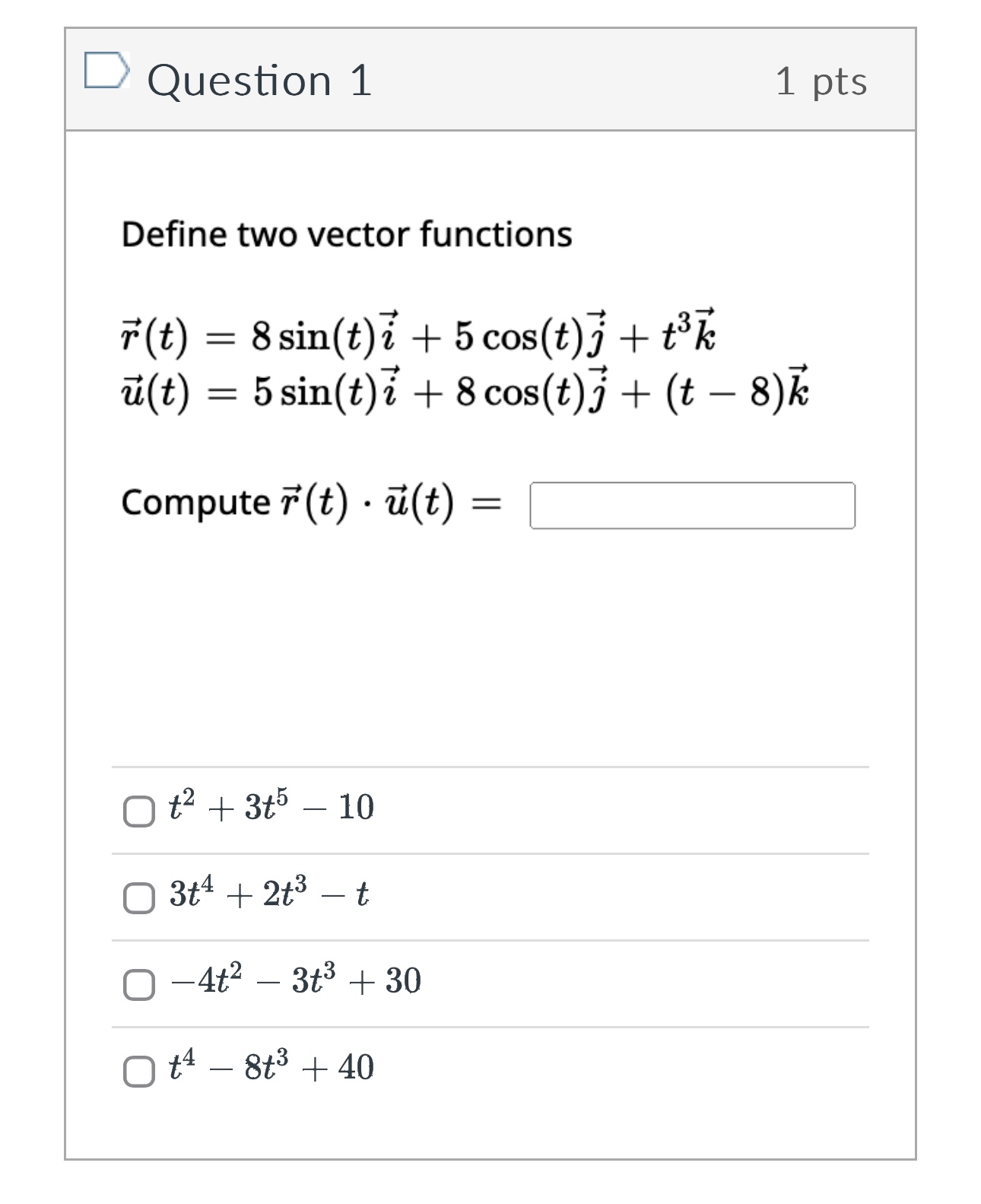
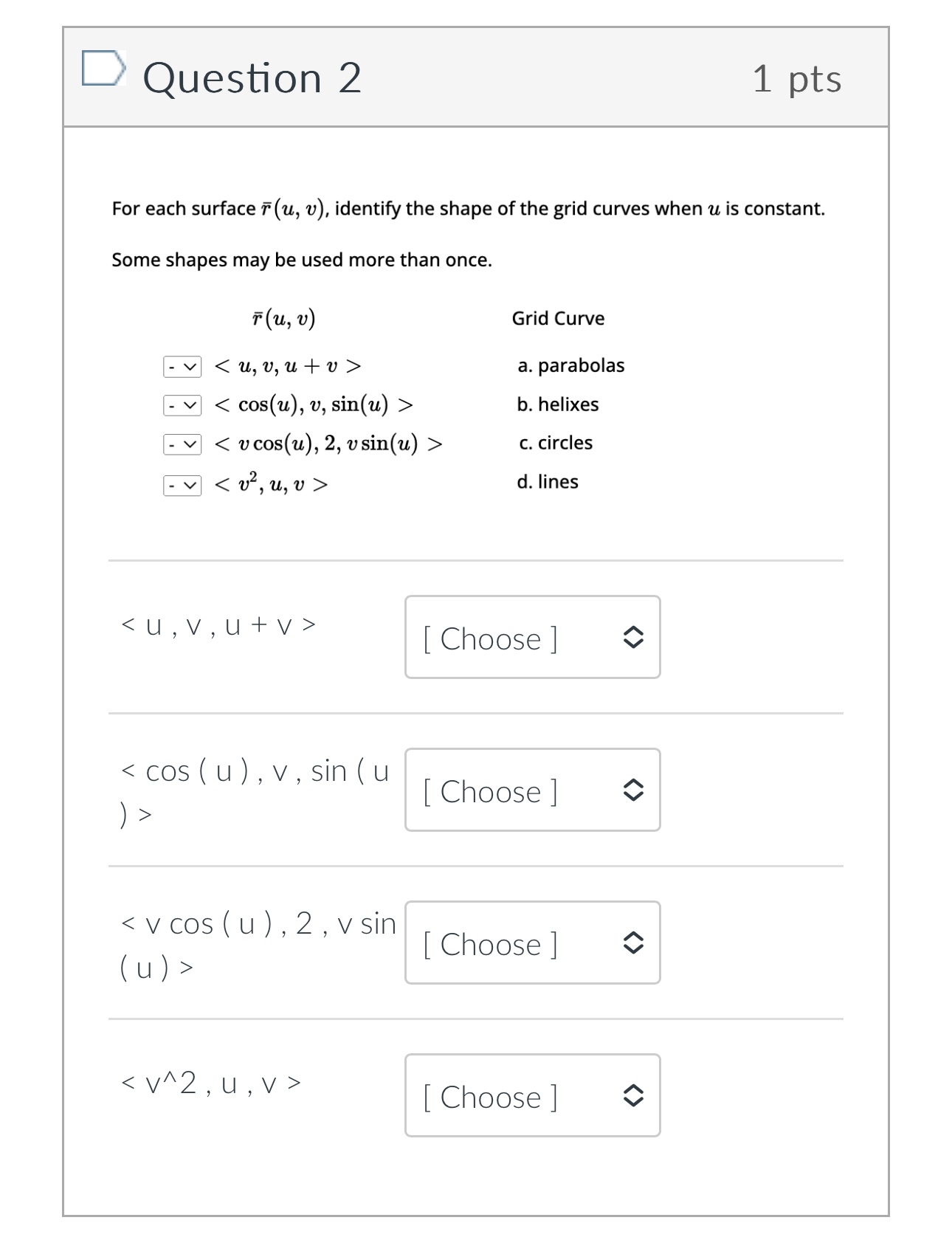
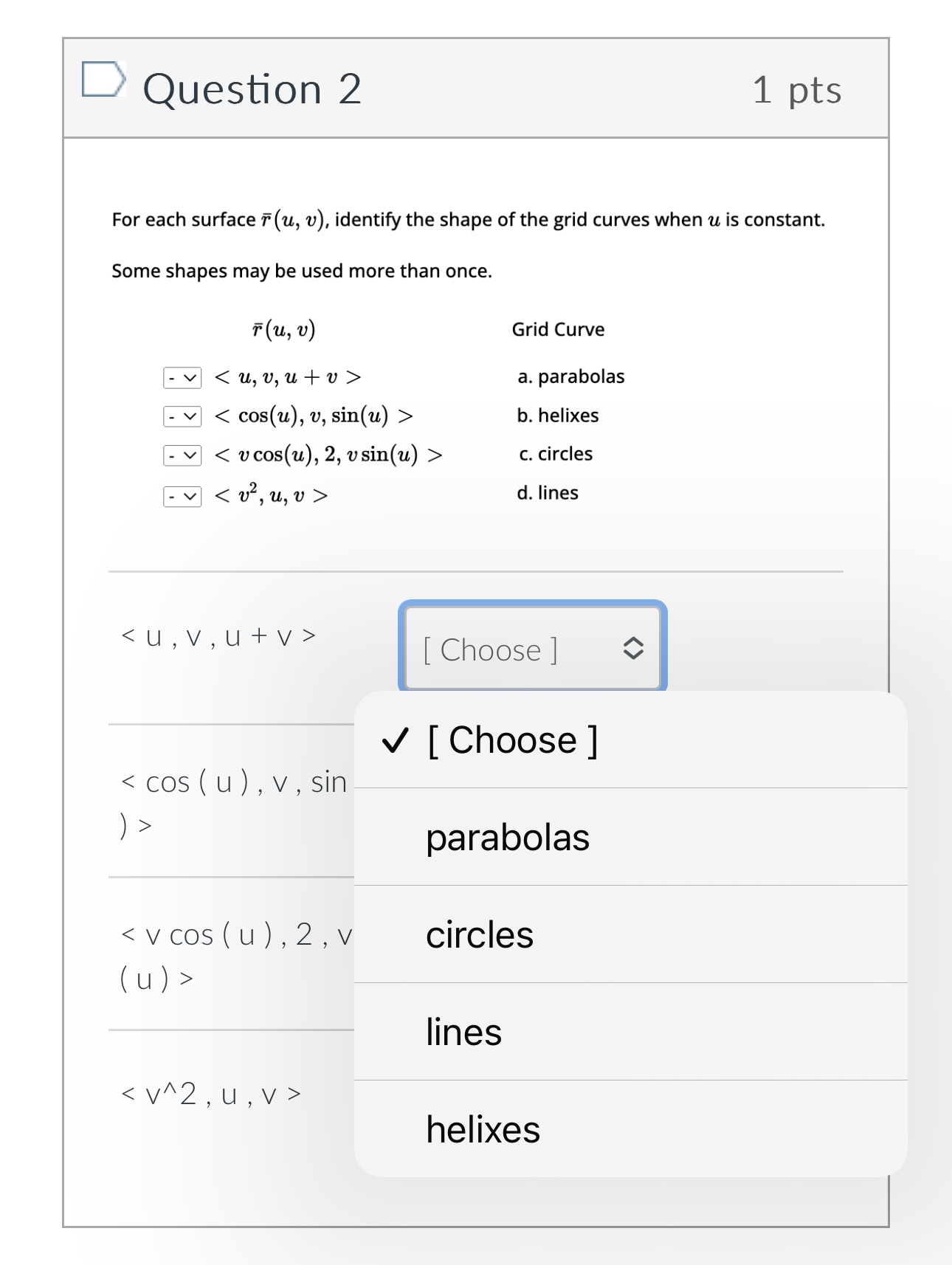
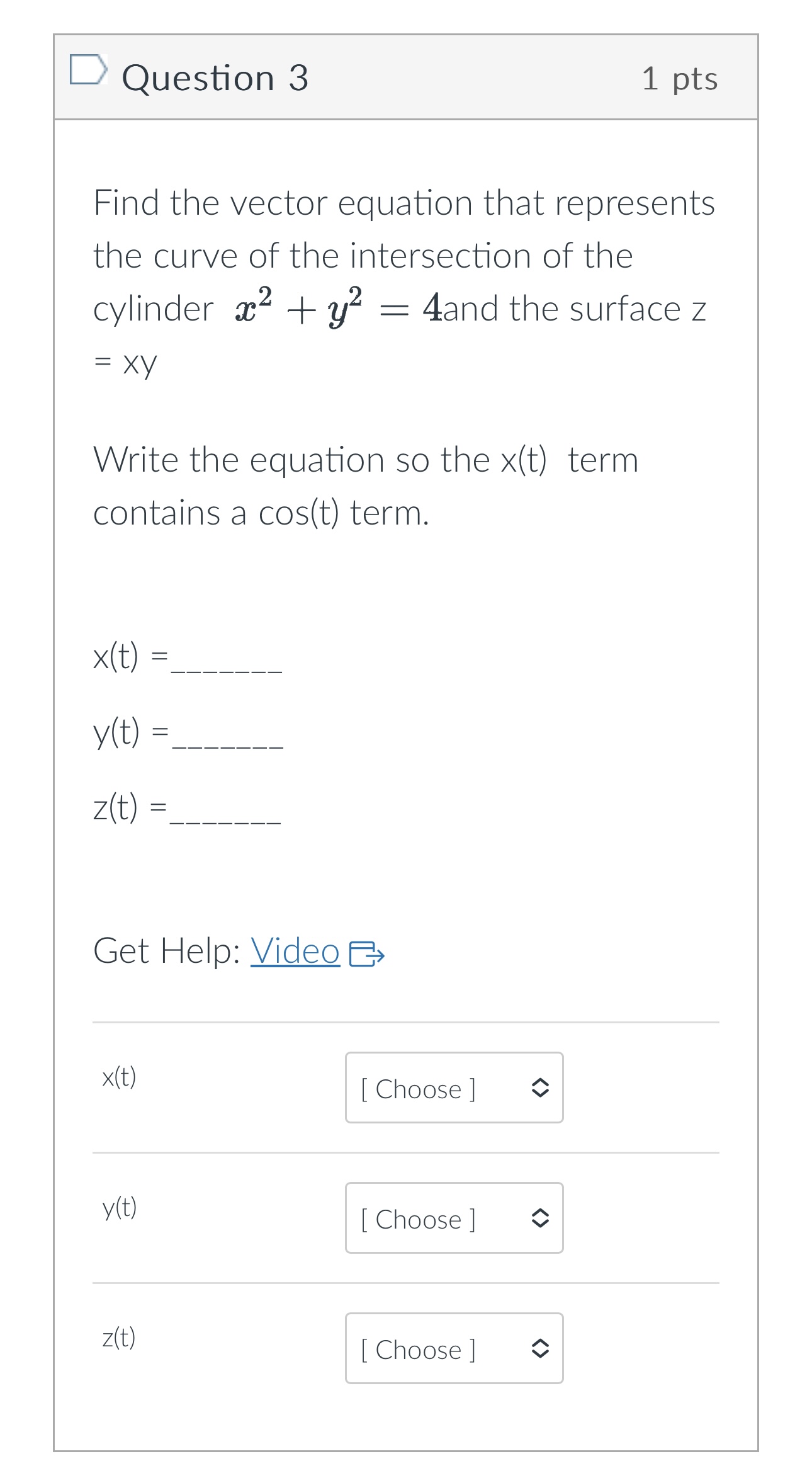
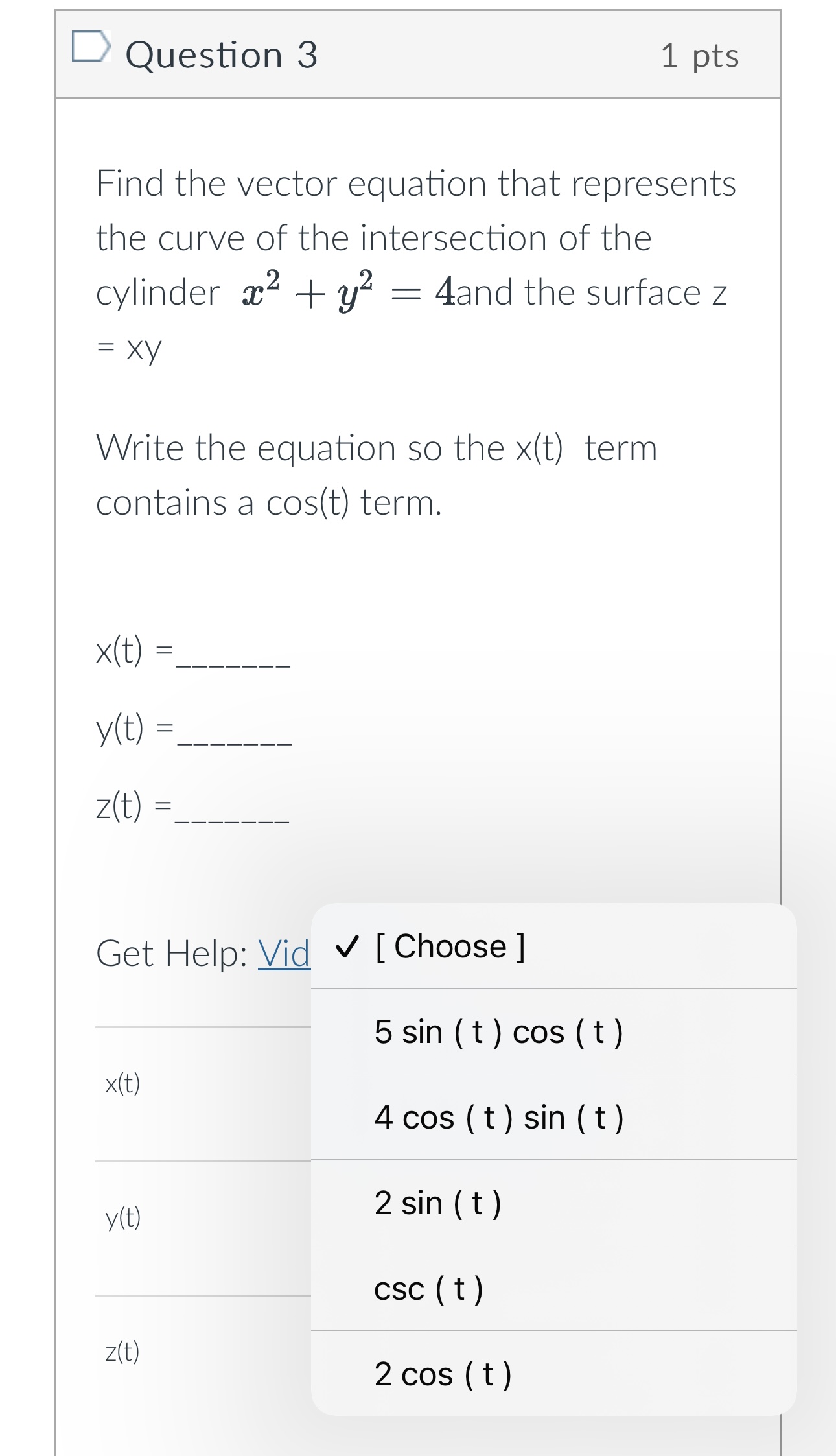
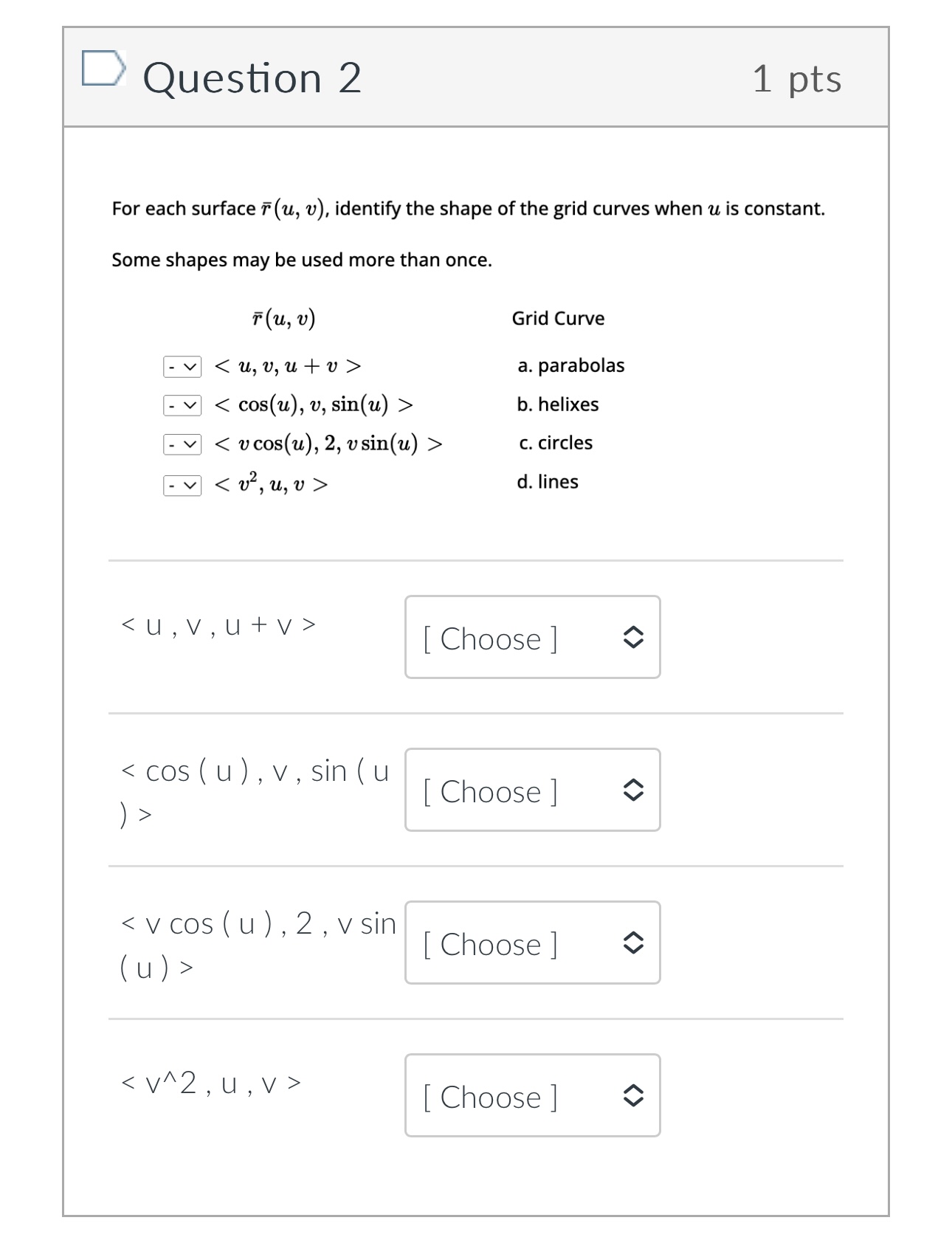
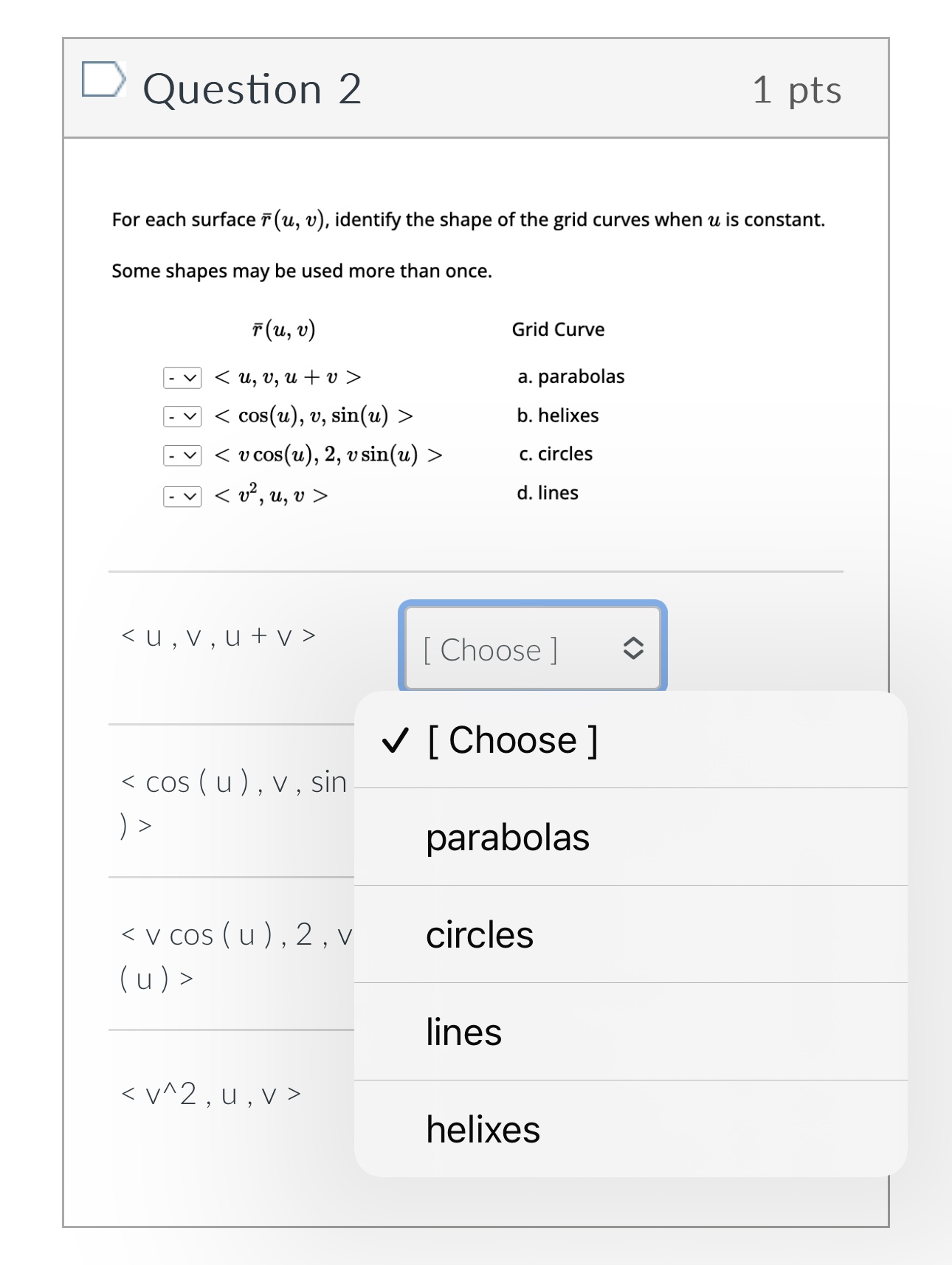
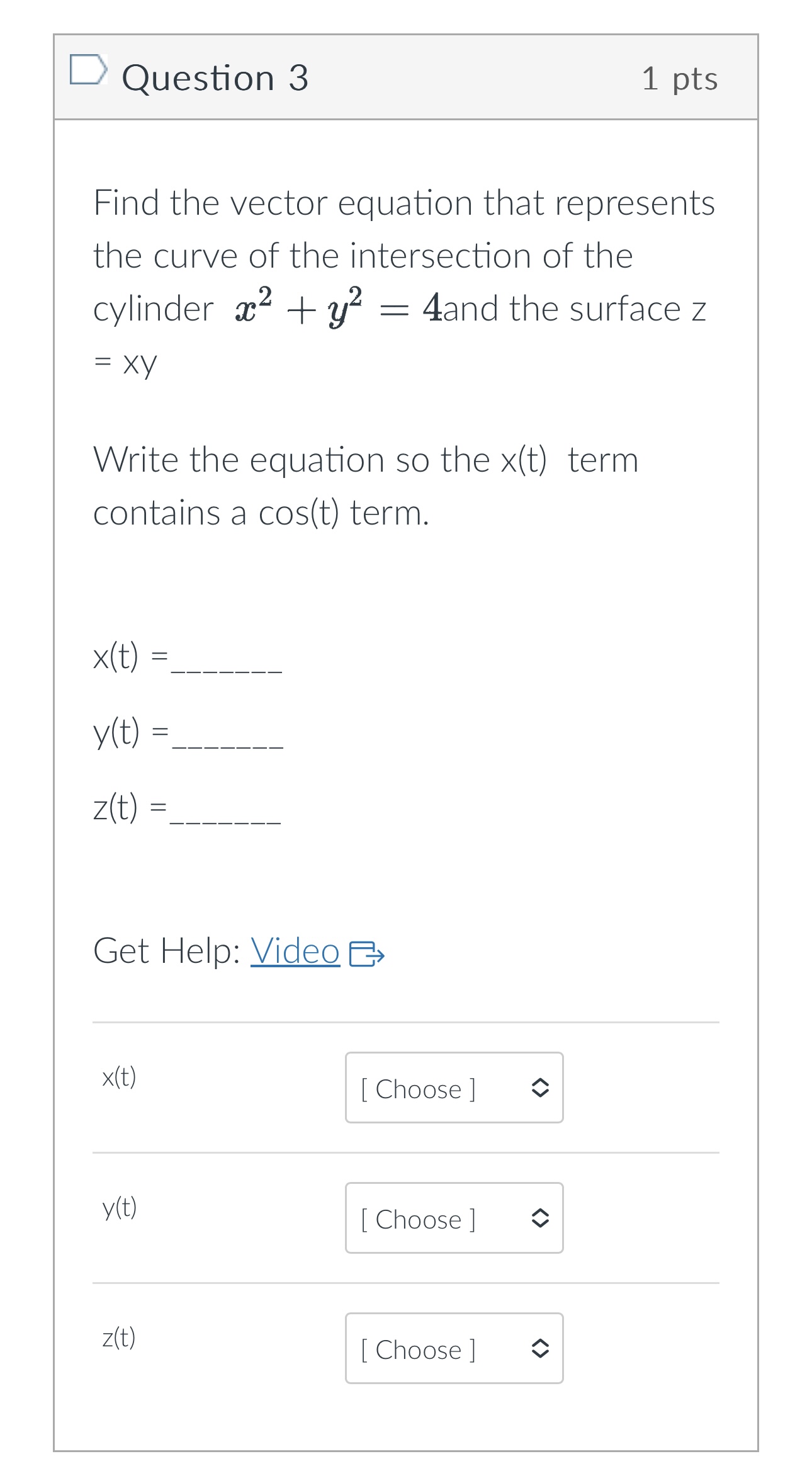
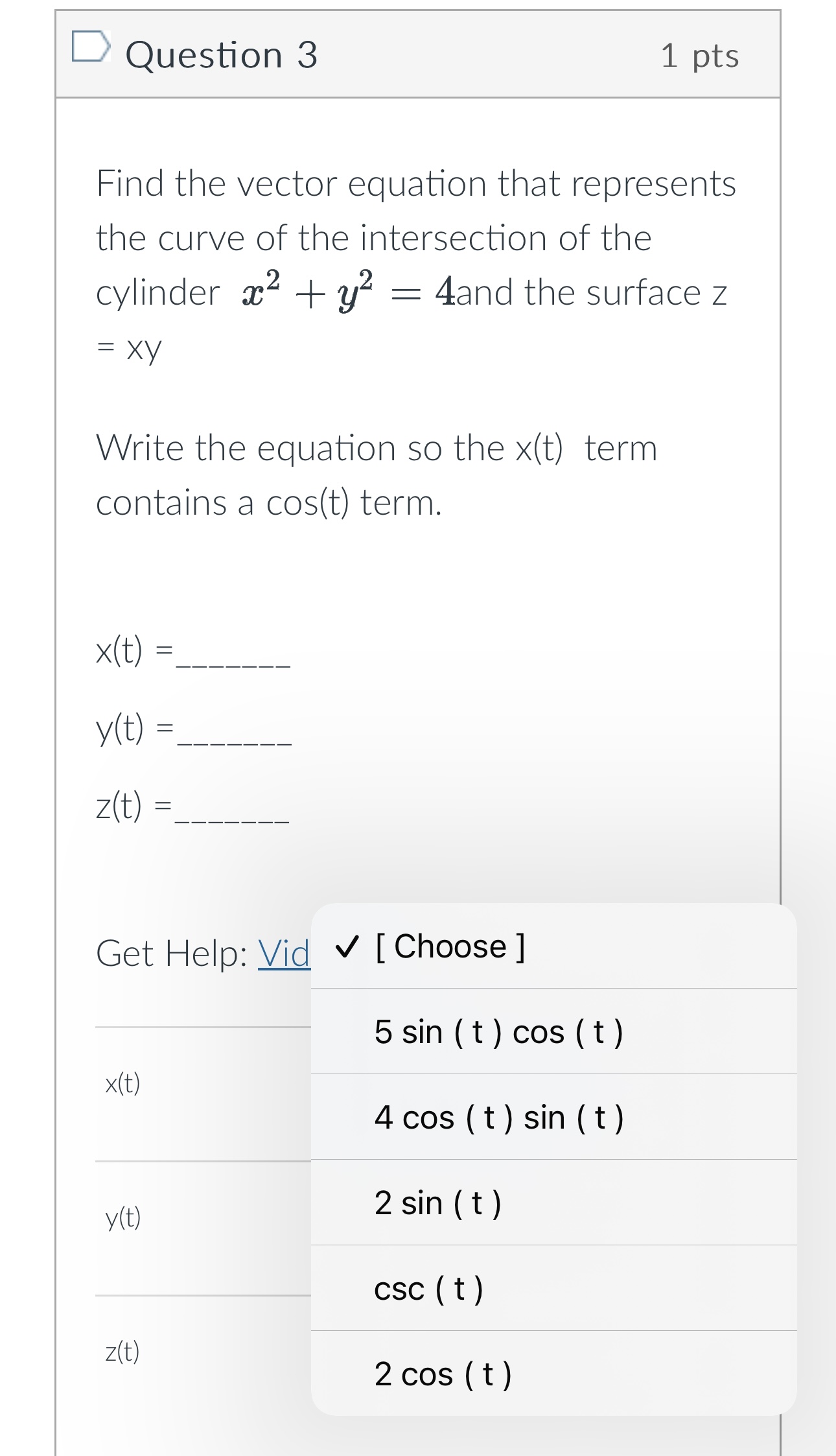
Question 1 1 pts Define two vector functions T (t) = 8 sin(t) i + 5 cos(t)3 + +3 k u(t) = 5 sin(t) i + 8 cos(t)j + (t - 8) k Compute T (t) . u(t) = Oth + 3+5 - 10 O 3t4 + 2+3 - t O -4t2 - 3+3 + 30 O t - 8+3 + 40Question 2 1 pts For each surface T (u, v), identify the shape of the grid curves when u is constant. Some shapes may be used more than once. T (u , V ) Grid Curve - v a. parabolas - v b. helixes - v c. circles - v d. lines [ Choose ] [ Choose ]Question 2 1 pts For each surface T (u, v), identify the shape of the grid curves when u is constant. Some shapes may be used more than once. T ( u , V ) Grid Curve - v a. parabolas - v b. helixes c. circles d. lines [ Choose ] [ Choose ] lines helixesQuestion 3 1 pts Find the vector equation that represents the curve of the intersection of the cylinder ac2 + 2 = 4and the surface z = XY Write the equation so the x(t) term contains a cos(t) term. x (t) = y(t) = z (t ) = Get Help: Video Ex x(t) [ Choose ] y (t) [ Choose ] z(t ) [ Choose ][:3 Question 3 1 pts Find the vector equation that represents the curve of the intersection of the cylinder :32 + :92 : 4and the surface 2 Write the equation so the >
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


