Please help

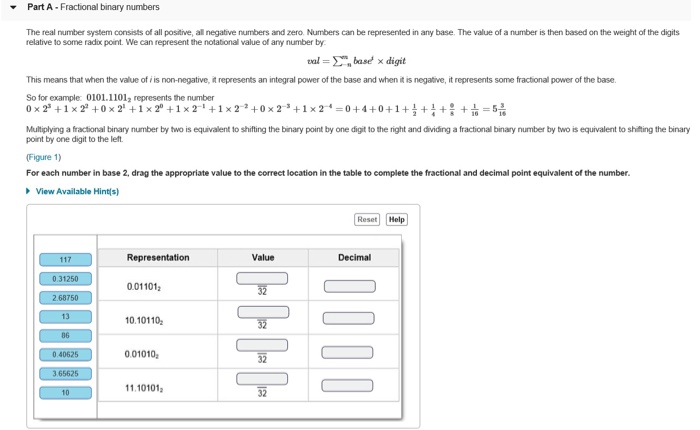
Part A Fractional binary numbers The real number system consists of all positive, all negative numbers and zero. Numbers can be represented in any base. The value of a number is then based on the weight of the digits relative to some radx point. We can represent the notational value of any number by al-base x digit This means that when the value of i is non-negative, it represents an integral power of the base and when it is negative, it represents some fractional power of the base. So for example: 0101.11012 represents the number Multiplying a fractional binary number by two is equivalent to shifting the binary point by one digit to the right and dividing a fractionall binary number by two is equivalent to shifting the binary point by one digit to the left (Figure 1) For each number in base 2, drag the appropriate value to the correct location in the table to complete the fractional and decimal point equivalent of the number. View Available Hinds) Reset Help Representation 0011012 0.10110 Value Decimal 0.31250 2.68750 13 0 40625001010 3 656 1.10101 10 32