please help

please gill up the last page. the exercise name is "MOLAR MASSOF A CONDENSABLE VAPOR" Thank you

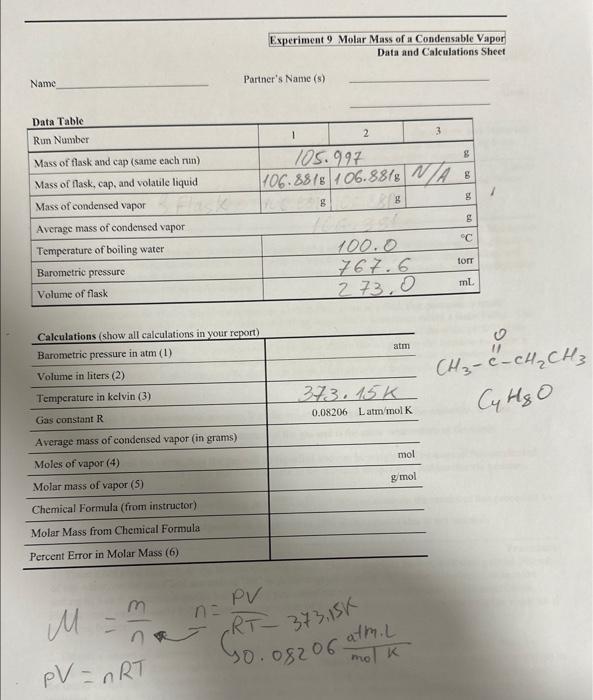
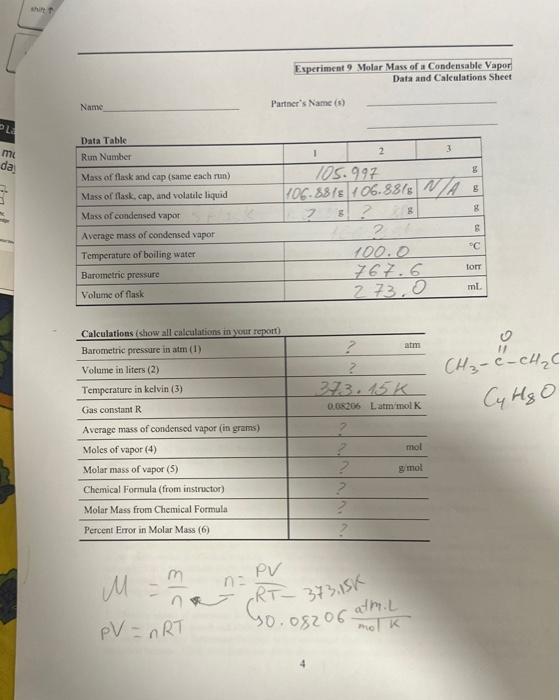
M=nmn=RTPV373,15G P0.08206molatmm/k The Melar Mass of a Condensable Vapor Reading assignment: Chang, Chemistry, 10e edition, Pp. 85-87; 185-187. To determine the molar mass of a condensable vapor through use of the ideal gas law. Equipment and Materials Hot plate, ring stand, analytical balance, 1-L beaker, 250 -mL round bottom flask, tap water, 5cm by 5 -cm picce of aluminum foil, 5-mL, of a volatile organic liquid (methyl cthyl ketone or ethyl acctate). Safety glasses or goggles are required for this experiment. Heating should take place in a furne bood. Waste must be disposed of in an organic chemicals waste container. The molar mass of a condensable vapor can be determined by adding an excess of the corresponding liquid to a weighed bulb, henting the assembly to volatilize all the liquid and to expel the excess vapor, cooling, and then weighing the bulb with the condensed vapor. We will use one of two organic liquids, either methyl ethyl ketone (MEK) or ethyl acetate (EA) to study. In this experiment we place a liquid that possesses a low boiling point in a flask that possesses a small opening. The flask is then placed into a beaker of boiling water (this is sometimes called a water bath). The Water both ensures that the temperature of the gas is the same as the botling point of the water (100= C if the barometrie pressure is 1 atm). The small opening in the flask allows the vapor from the liquid to excape at a controlled rate and ensures that the pressure of the vapor in the container is cqual to the barometric pressure. The ideal gas law (PV - nRT) eas then be used to determine the number of moles of a gas that occupics the container: n=RTPV where P is the barometric pressure. V is the volume of the gas occupying the container, R is the universal gas constant, and T is the temperature of the gis and is the same iemperature as the water. If we rupidly cool the vapor, then the gas will be liqueficd and can be wciehed. The mass of this condensed vapor is equal to the mass of vapor that fills the flask at the elevated temperafure and barometric pressure: The molar mass of the liquid/vapor is then M=molesmass=nm. We can corripare the results of this procodure po. the known molar mass of the compound. A result within 208 is of the actual value is not unusual. Procedare 1. Place a hot plate squarely at the bottom of a ring stand. Place a one-liter beaker, containing about 700ml. of tap water, on the plate and use setting "HI" to achieve quick heating. When the water boils, reduse the setling to 5 or 6 to maintain gentle boiling until you complete all macs meaghremenss in this cxperiment. Place a small vessel nearly full of water oa one corner of the plate, for later une in maintaininethe water level in the big beaker. 2. Obtain a square of aluminum foil (about 5cm on a side), and fashion a cap for your 250ml. flask by laying the foil on the mouth and folding down the sides. With a pin, poke a tiny hole (as small as pussible) in the center of the cap. Determine the mass of the unwashed flask with cap to the nearet 0.1 mg wsint the anulytical balance. From your instractor obtain aboat 3mL of an unknown liquid (which cuptains a fea milligrams of dye to help you see the liquid's disappearance) in the flask. Replace the cap securely. Do not weigh the flask at this point. 3. Clamp the flask on its lip and place the flask as far down in the beaker as the clamp permits. Fix the clamp to the pole so that the flask is tilted enough to concentrate its liquid in one "corner." Also record the barometric pressure. 4. As the water boils, watch the liquid in the flask. One minute after all of the liquid appears to have evaporated, remove the flask and clamp from the pole. Allow cool tap water to run over the flask, being careful that no water gets on or under the foil cap. Use paper towels to dry the flask and to dab the foil in case any water droplets are on it. Weigh the flask, cap, and condensed unknown liquid. Be sure to readjust the water level in the beaker to about 700mL. 5. Without pouring the liquid out of the flask, add more of the liquid to the flask (perhaps 1mL ) so that you have a similar amount of liquid as you did earlier. Then proceed as you did with the first sample (re-do steps 3 and 4). If your two weights of condensed vapor differ by more than 0.05g, you must obtain more liquid and repeat the procedure. Your two closest weights, those within 0.05g of each other, should be used to find the average mass of condensed vapor. 6. Dispose of the liquid (MEK or EA) in the organic waste container provided. Rinse the flask and fill it completely with tap water. The round bottom flask does not have a volume of 250mL. Measure the volume of the flask all the way to the top with a graduated cylinder to the nearest 1mL. Calculations 1. 1atm=760 torr 760mmHHg 2. 1mL=103 L. The ideal gas law uses volume in liters. 3. Tk=Tc+273.15 4. Use the idcal gas law for this calculation: PV=nRT 5. molar mass =molesofvapormassofvapor 6. Using the actual molar mass of your unknown (calculated from its formula), calculate the actual percent error of your molar mass determination. \% error =actualvalueactualvalue-measuredvalue100 After you have reported your calculated molar mass to the instructor, ask for the name or the formula of your unknown. 1. Calculate the molar mass of the condensable vapor. From the known molar mass calculate a percentage error. Show all calculations clearly on a separate piece of paper. 2. On a separate piece of paper describe (in one paragraph) the evidence that the liquid exists in gaseous form at room temperature. 3. Deseribe two or three ways in which the measurements you made could lead to errors in the results. Explain how each error would affect the answer of molar mass. In other words, would the molar mass go up or down and why? M=nmn=RT373.15PV PV=nRT