PLEASE HELP

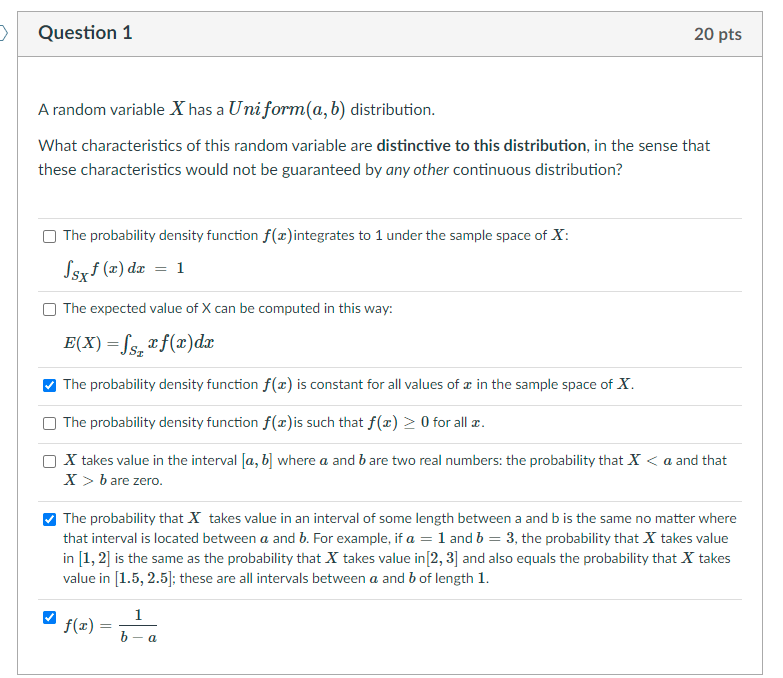
Question 1 20 pts A random variable X has a Uniform(a, b) distribution. What characteristics of this random variable are distinctive to this distribution, in the sense that these characteristics would not be guaranteed by any other continuous distribution? O The probability density function f(@)integrates to 1 under the sample space of X: Isxf (x) da = 1 O The expected value of X can be computed in this way: E(X) =Ss, xf(x)dx The probability density function f(x) is constant for all values of a in the sample space of X. The probability density function f(x) is such that f(x) > 0 for all x. O X takes value in the interval [a, b] where a and b are two real numbers: the probability that X bare zero. The probability that X takes value in an interval of some length between a and b is the same no matter where that interval is located between a and b. For example, if a = 1 and b = 3, the probability that X takes value in [1, 2] is the same as the probability that X" takes value in [2, 3] and also equals the probability that X takes value in [1.5, 2.5); these are all intervals between a and b of length 1. f ( I) = b - a