Please help question 21-26

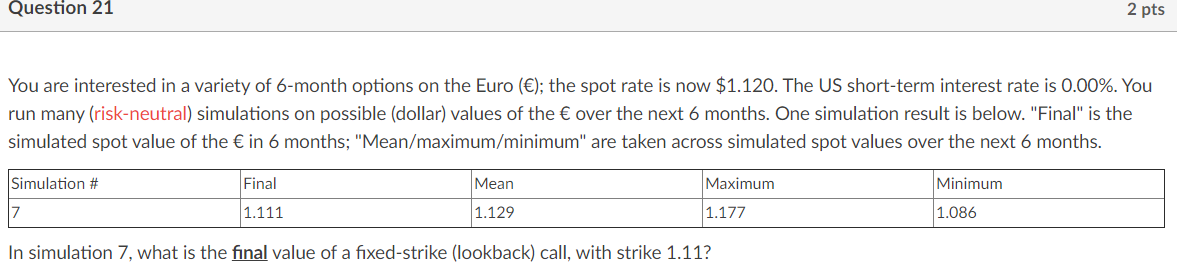
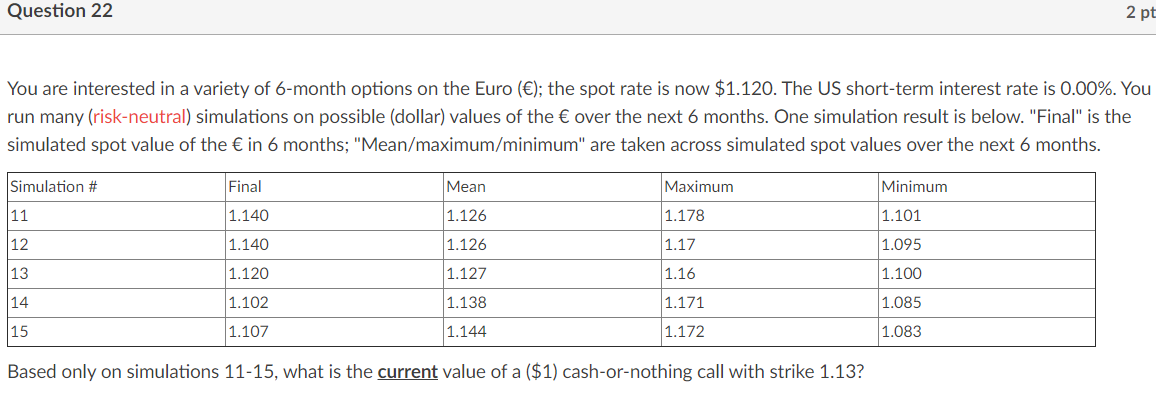
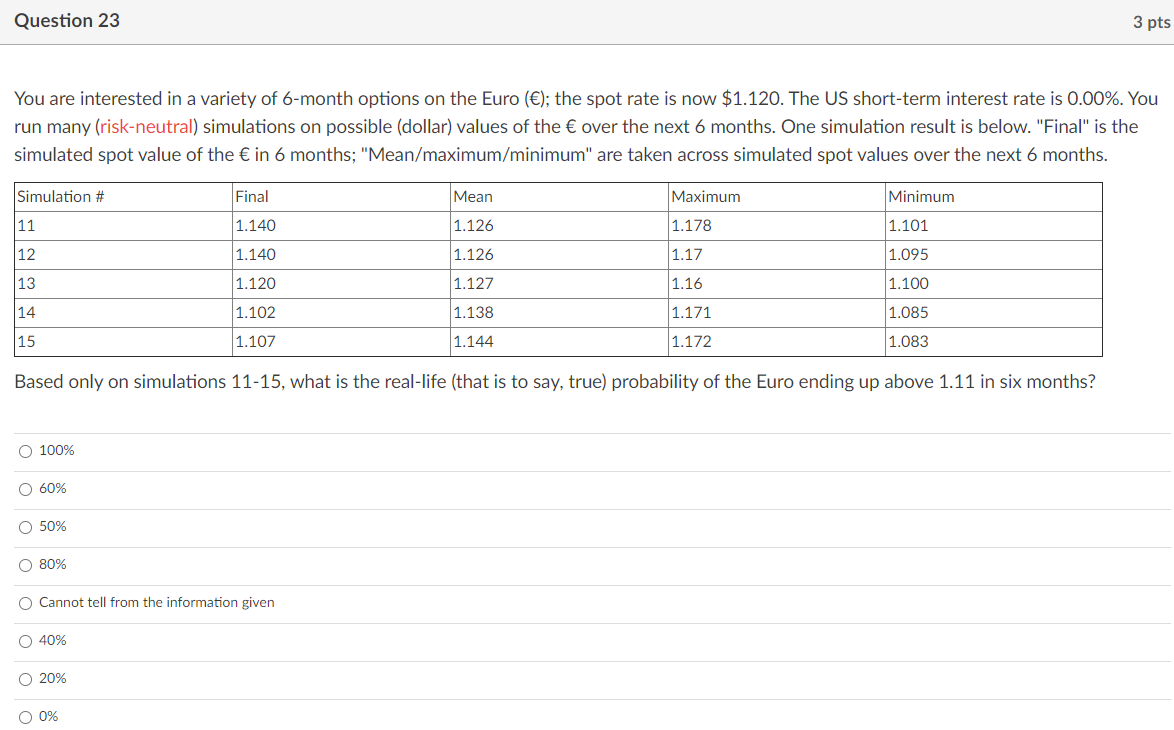
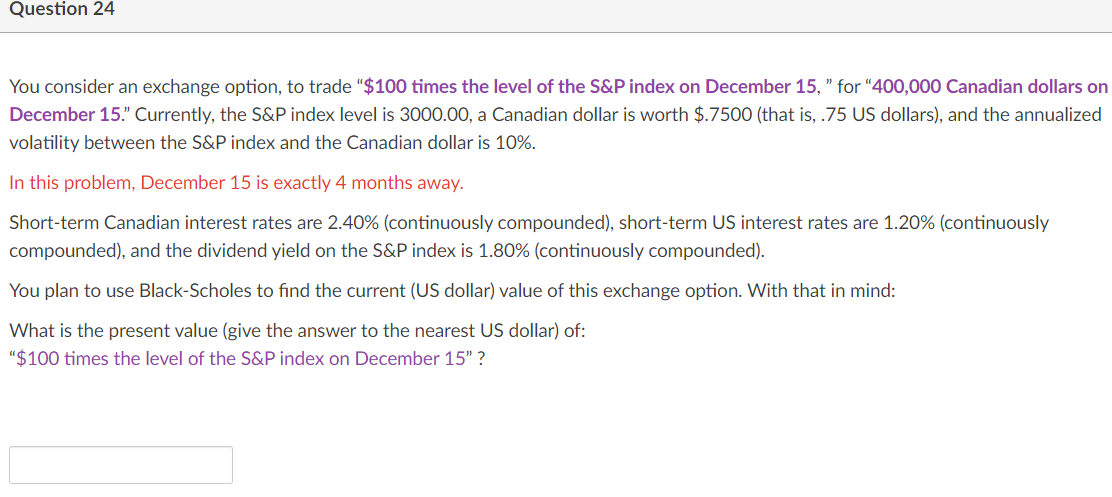
Question 21 2 pts You are interested in a variety of 6-month options on the Euro (l: the spot rate is now $1.120. The US short-term interest rate is 0.00%. You run many (riskneutral} simulations on possible (dollar) values of the over the next 6 months. One simulation result is below. "Final" is the simulated spot value of the in 6 months; "Meam'maximum/minimum" are taken across simulated spot values over the next 6 months. Simulation 3\" Final Mean Maximum Minimum 7 1.111 1.129 1.177 1.036 In simulation 7. what is the nal value of a xed-strike (lookbatkl call, with strike 1.11? Question 22 2 pt You are interested in a variety of 6-month options on the Euro (); the spot rate is now $1.120. The US short-term interest rate is 0.00%. You run many (riskneutral} simulations on possible (dollar) values of the over the next 6 months. One simulation result is below. "Final\" is the simulated spot value of the in 6 months; "Mean/maximumz'minimum" are taken across simulated spot values over the next 6 months. Simulation # Final Mean Maximum Minimum 11 1.140 1.126 1.173 1.101 12 1.140 1.126 1.17l 1.095 13 1.120 1.127 1.16 1.100 14 1.102 1.133 1.171 1.035 15 1.107 1.144 1.172 1.033 Based only on simulations 11-15, what is the current value of a ($1) cash-or-nothing call with strike 1.13? Question 23 3 pts You are interested in a variety of 6-month options on the Euro (l; the spot rate is now $1.120. The US short-term interest rate is 0.00%. You run many (riskneutral} simulations on possible (dollar) values of the over the next 6 months. One simulation result is below. "Final" is the simulated spot value of the in 6 months; "Mean/maximumIminimum" are taken across simulated spot values over the next 6 months. Simulation a\" Final Mean Maximum Minimum 11 1.140 1.126 1.173 1.101 12 1.140 1.126 1.17 1.095 13 1.120 1.127 1.16 1.100 14 1.102 1.133 1.171 1.035 15 1.107 1.144 1.172 1.033 Based only on simulations 11-15, what is the real-life (that is to say. true) probability of the Euro ending up above 1.11 in six months? 0 100% O 60% O 50% O 80% 0 Cannot tell from the information given 0 40% O 20% 00% Question 24 You consider an exchange option, to trade "$100 times the level of the S&P index on December 15, " for "400,000 Canadian dollars on December 15.\" Currently, the S&P index level is 3000.00, a Canadian dollar is worth $.7500 (that is, .75 US dollars], and the annualized volatility between the S&P index and the Canadian dollar is 10%. In this problem, December 15 is exactly 4 months away. Short-term Canadian interest rates are 2.40% {continuously compounded], short-term US interest rates are 1.20% {continuously compounded). and the dividend yield on the S&P index is 1.80% (continuously compounded). You plan to use Black-Scholes to nd the current (US dollar] value of this exchange option. With that in mind: What is the present value (give the answer to the nearest US dollar] of: "$100 times the level of the S&P index on December 15" ? Question 25 You consider an exchange option, to trade \"$100 times the level of the S&P index on December 15, " for "400,000 Canadian dollars on December 15.\" Currently, the S&P index level is 3000.00, a Canadian dollar is worth $.7500 (that is, .75 US dollars], and the annualized volatility between the S&P index and the Canadian dollar is 10%. In this problem, December 15 is exactly 7 months away. Short-term Canadian interest rates are 2.40% (continuously compounded], short-term US interest rates are 1.20% (continuously compounded). and the dividend yield on the S&P index is 1.80% (continuously compounded). You plan to use Black-Scholes to nd the current (US dollar] value of this exchange option. With that in mind: What is the present value (give the answer to the nearest US dollar] of: "400,000 Canadian dollars on December 15" ? Question 26 Today is March 15. You consider an exchange option, to trade "$100 times the level of the S&P index on December 15, \" for \"400,000 Canadian dollars on December 15.\" Currently, the S&P index level is 3000.00, a Canadian dollar is worth $.7500 (that is, .75 US dollars}, and the annualized volatility between the S&P index and the Canadian dollar is 10%. In this problem, December 15 is exactly 9 months away. Short-term Canadian interest rates are 2.40% (continuously compounded], short-term US interest rates are 1.20% (continuously compounded). and the dividend yield on the S&P index is 1.80% (continuously compounded). You plan to use Black-Scholes to nd the current (US dollar] value of this exchange option. With that in mind: What is the total volatility over the life of the option? (Give this answer in percentage terms, and to four digits. For example, if your answer is "12.34%", enter "12.34")