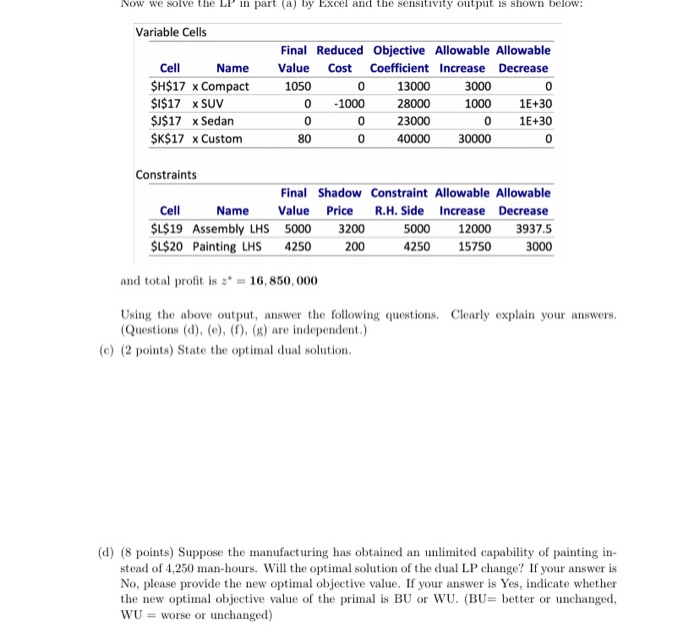
Question: please help show how to solve D, E, F and G. 2. (50 points) A car manufacturer produces 4 types of cars: compact, SUV, sedan,
please help show how to solve D, E, F and G.

2. (50 points) A car manufacturer produces 4 types of cars: compact, SUV, sedan, and custom, with sale prices set to $13,000, $28,000, $23,000 and $40,000 respectively. The manufacturing process involves two major steps: assembly and painting. The required numbers of hours per type of car are as follows: Assembly Painting Compact SUV Sedan Custom 4 1 40 The manufacturer needs a production plan for one year in which there are 5,000 hours available for assembly and 4,250 man-hours for painting. (a) (6 points) Using 2 = units of type i cars to produce, i = compact, SUV, sedan, and custom, formulate an LP (assuming this company can produce fractional number of to determine an optimal manufacturing plan to maximize total revenue (b) (10 points) Write the dual of the LP in part (a). Now we solve the LP in part (a) by Excel and the sensitivity output is shown below: Variable Cells Cell Name $H$17 X Compact $I$17 x SUV $J$17 x Sedan $K$17 x Custom Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 1050 0 13000 3000 0 - 1000 28000 1000 1 E+30 0 0 23000 0 1E+30 800 40000 30000 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $L$19 Assembly LHS 5000 3200 5000 12000 3937.5 $L$20 Painting LHS 4250 2 00 4250 15750 3 000 and total profit is * = 16,850,000 Using the above output, answer the following questions. Clearly explain your answers. (Questions (d), (e), (6), (g) are independent.) (e) (2 points) State the optimal dual solution. (d) (8 points) Suppose the manufacturing has obtained an unlimited capability of painting in stead of 4,250 man-hours. Will the optimal solution of the dual LP change? If your answer is No, please provide the new optimal objective value. If your answer is yes, indicate whether the new optimal objective value of the primal is BU or WU. (BU= better or unchanged, WU = worse or unchanged) (e) (8 points) The manufacturer can pay $3,000,000 to rent a new machine to increase the assembly capacity (ie, assembly hours) by 30%. Alternatively, the manufacturer can pay overtime hours to the workers to increase the assembly capacity by 30%. In this way, the manufacturer can pay overtime hours up to 20% of current capacity at extra $1,600/hour, and above 20% (i.e., from 20% to 30%) at $3,000/hour. Is it better to rent a machine or pay overtime? (f) (8 points) What can the largest sales price for SUV be such that it is not worthwhile to produce i.e., SUV stays zero)? (8) (8 points) The company is considering introducing electric car to be sold for $18,000, re- quiring 6 hour for assembly and 2 hours for painting. Is it worthwhile to produce this type of cars? If your answer is No, please explain. If your answer is Yes, indicate whether the new optimal objective value of the primal is BU or WU. (BU= better or unchanged, WU- worse or unchanged) 2. (50 points) A car manufacturer produces 4 types of cars: compact, SUV, sedan, and custom, with sale prices set to $13,000, $28,000, $23,000 and $40,000 respectively. The manufacturing process involves two major steps: assembly and painting. The required numbers of hours per type of car are as follows: Assembly Painting Compact SUV Sedan Custom 4 1 40 The manufacturer needs a production plan for one year in which there are 5,000 hours available for assembly and 4,250 man-hours for painting. (a) (6 points) Using 2 = units of type i cars to produce, i = compact, SUV, sedan, and custom, formulate an LP (assuming this company can produce fractional number of to determine an optimal manufacturing plan to maximize total revenue (b) (10 points) Write the dual of the LP in part (a). Now we solve the LP in part (a) by Excel and the sensitivity output is shown below: Variable Cells Cell Name $H$17 X Compact $I$17 x SUV $J$17 x Sedan $K$17 x Custom Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 1050 0 13000 3000 0 - 1000 28000 1000 1 E+30 0 0 23000 0 1E+30 800 40000 30000 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $L$19 Assembly LHS 5000 3200 5000 12000 3937.5 $L$20 Painting LHS 4250 2 00 4250 15750 3 000 and total profit is * = 16,850,000 Using the above output, answer the following questions. Clearly explain your answers. (Questions (d), (e), (6), (g) are independent.) (e) (2 points) State the optimal dual solution. (d) (8 points) Suppose the manufacturing has obtained an unlimited capability of painting in stead of 4,250 man-hours. Will the optimal solution of the dual LP change? If your answer is No, please provide the new optimal objective value. If your answer is yes, indicate whether the new optimal objective value of the primal is BU or WU. (BU= better or unchanged, WU = worse or unchanged) (e) (8 points) The manufacturer can pay $3,000,000 to rent a new machine to increase the assembly capacity (ie, assembly hours) by 30%. Alternatively, the manufacturer can pay overtime hours to the workers to increase the assembly capacity by 30%. In this way, the manufacturer can pay overtime hours up to 20% of current capacity at extra $1,600/hour, and above 20% (i.e., from 20% to 30%) at $3,000/hour. Is it better to rent a machine or pay overtime? (f) (8 points) What can the largest sales price for SUV be such that it is not worthwhile to produce i.e., SUV stays zero)? (8) (8 points) The company is considering introducing electric car to be sold for $18,000, re- quiring 6 hour for assembly and 2 hours for painting. Is it worthwhile to produce this type of cars? If your answer is No, please explain. If your answer is Yes, indicate whether the new optimal objective value of the primal is BU or WU. (BU= better or unchanged, WU- worse or unchanged)