Please help solve missing parts thank you

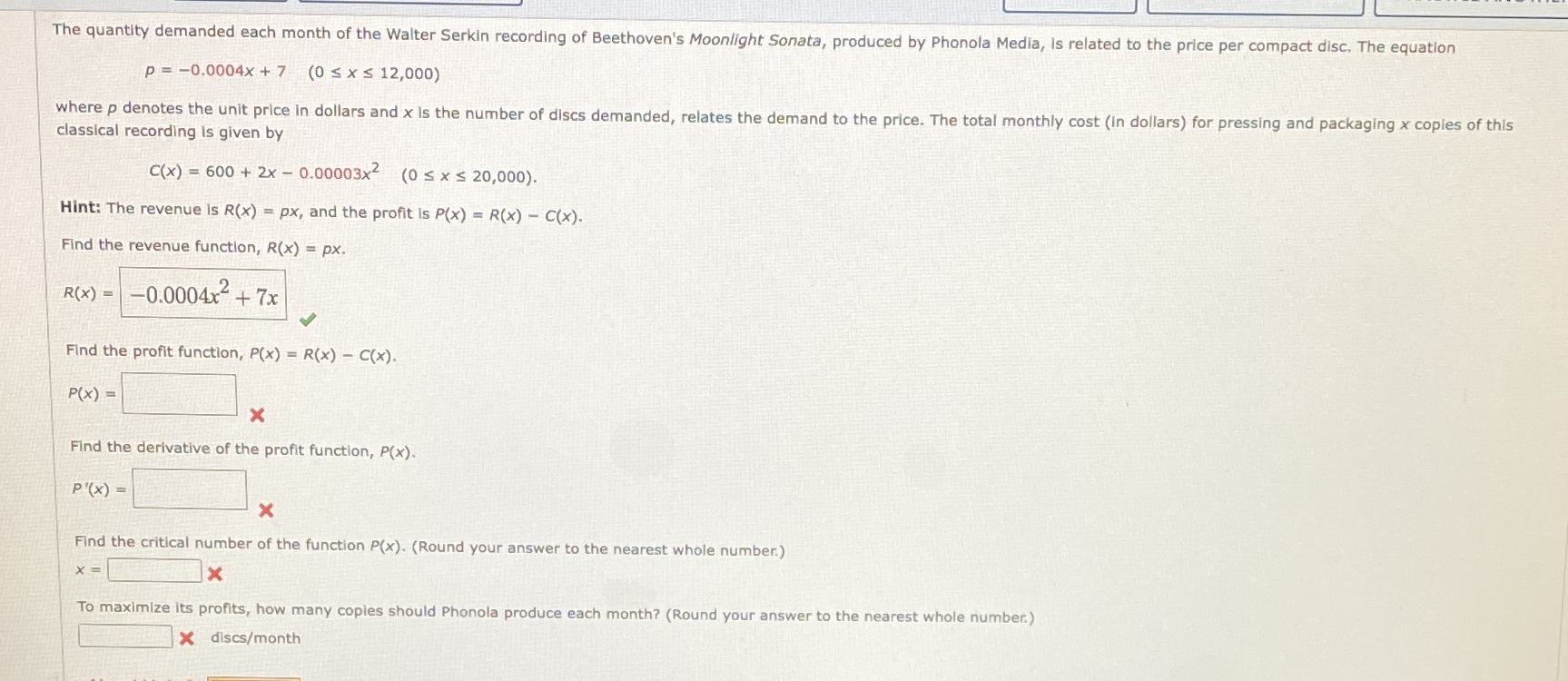
The quantity demanded each month of the Walter Serkin recording of Beethoven's Moonlight Sonata, produced by Phonola Media, Is related to the price per compact disc. The equation p = -0.0004x + 7 (0 S x 5 12,000) where p denotes the unit price in dollars and x Is the number of discs demanded, relates the demand to the price. The total monthly cost (in dollars) for pressing and packaging x copies of this classical recording is given by C(x) = 600 + 2x - 0.00003x2 (0 5 x s 20,000). Hint: The revenue is R(x) = px, and the profit is P(x) = R(x) - C(x). Find the revenue function, R(x) = px. R(x) = -0.0004x + 7x Find the profit function, P(x) = R(x) - C(x). P(X ) = X Find the derivative of the profit function, P(x). P' ( x) = X Find the critical number of the function P(x). (Round your answer to the nearest whole number.) X = X To maximize Its profits, how many copies should Phonola produce each month? (Round your answer to the nearest whole number.) X discs/month