please help solve the question in python only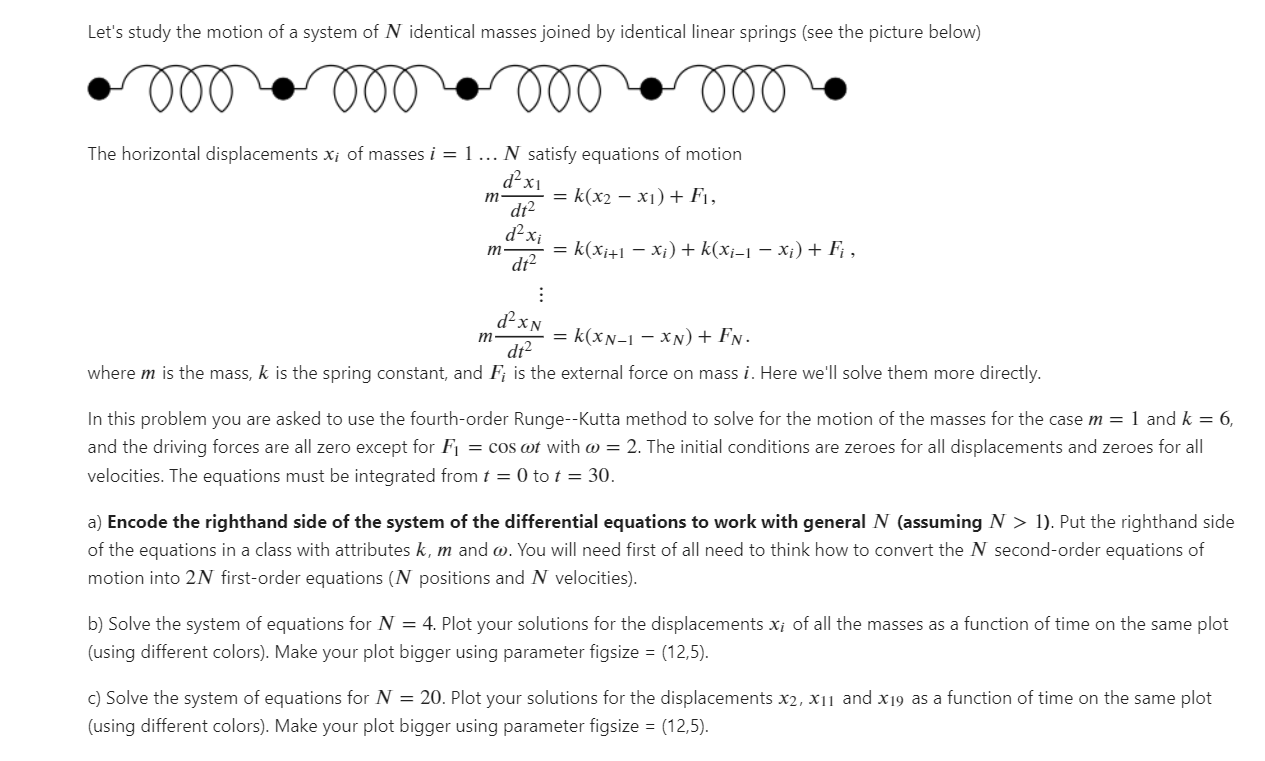

Let's study the motion of a system of N identical masses joined by identical linear springs (see the picture below) 000 000 000 000 The horizontal displacements Xi of masses i = 1... N satisfy equations of motion daxi dt2 = k(x2 xi) + F1, m- dxi m = k(Xi+1 xi) + k(Xi-1 - Xi) + Fi, dt2 dxn m = k(xN-1 - XN) + FN. dt2 where m is the mass, k is the spring constant, and Fi is the external force on mass i. Here we'll solve them more directly. In this problem you are asked to use the fourth-order Runge--Kutta method to solve for the motion of the masses for the case m = 1 and k = 6, and the driving forces are all zero except for F1 = cos ot with o = 2. The initial conditions are zeroes for all displacements and zeroes for all velocities. The equations must be integrated from t = 0 to t = 30. a) Encode the righthand side of the system of the differential equations to work with general N (assuming N > 1). Put the righthand side of the equations in a class with attributes k, m and o. You will need first of all need to think how to convert the N second-order equations of motion into 2N first-order equations (N positions and N velocities). b) Solve the system of equations for N = 4. Plot your solutions for the displacements Xi of all the masses as a function of time on the same plot (using different colors). Make your plot bigger using parameter figsize = (12,5). c) Solve the system of equations for N = 20. Plot your solutions for the displacements X2, X11 and X19 as a function of time on the same plot (using different colors). Make your plot bigger using parameter figsize = (12,5). Let's study the motion of a system of N identical masses joined by identical linear springs (see the picture below) 000 000 000 000 The horizontal displacements Xi of masses i = 1... N satisfy equations of motion daxi dt2 = k(x2 xi) + F1, m- dxi m = k(Xi+1 xi) + k(Xi-1 - Xi) + Fi, dt2 dxn m = k(xN-1 - XN) + FN. dt2 where m is the mass, k is the spring constant, and Fi is the external force on mass i. Here we'll solve them more directly. In this problem you are asked to use the fourth-order Runge--Kutta method to solve for the motion of the masses for the case m = 1 and k = 6, and the driving forces are all zero except for F1 = cos ot with o = 2. The initial conditions are zeroes for all displacements and zeroes for all velocities. The equations must be integrated from t = 0 to t = 30. a) Encode the righthand side of the system of the differential equations to work with general N (assuming N > 1). Put the righthand side of the equations in a class with attributes k, m and o. You will need first of all need to think how to convert the N second-order equations of motion into 2N first-order equations (N positions and N velocities). b) Solve the system of equations for N = 4. Plot your solutions for the displacements Xi of all the masses as a function of time on the same plot (using different colors). Make your plot bigger using parameter figsize = (12,5). c) Solve the system of equations for N = 20. Plot your solutions for the displacements X2, X11 and X19 as a function of time on the same plot (using different colors). Make your plot bigger using parameter figsize = (12,5)