Please help solving last questions

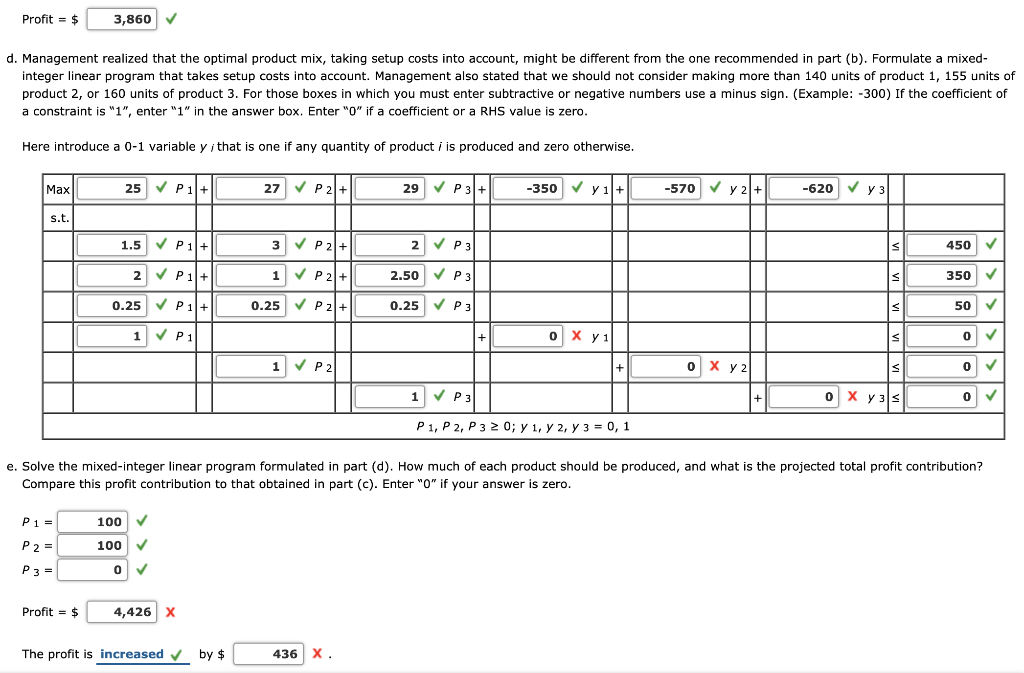
Problem 7-11 (Algorithmic) Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows: Department Product 1 Product 2 Product 3 A 1.50 3.00 2.00 B 2.00 1.00 2.50 C 0.25 0.25 0.25 During the next production period, the labor-hours available are 450 in department A, 350 in department B, and 50 in department C. The profit contributions per unit are $25 for product 1, $27 for product and $29 for product 3. Use a software package LINGO. a. Formulate an integer linear programming model for maximizing total profit contribution. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300) If constant is "1", it must be entered in the box. Let P; = units of product i produced Max 25 P 1 + 27 P2 + 29 P3 s.t. 1.5 P 1 + 3 P2 + 2 P315 450 2 P1+ 1 P 2 + 2.50 P35 350 0.25 P 1 + 0.25 P 21+ 0.25 P35 50 P1, P2, P320 b. Solve the integer linear program formulated in part (a). How much of each product should be produced, and what is the projected total profit contribution? Pi= 60 P 2 = 80 P 3 = 60 Profit = $ 5,400 Profit = $ 3,860 d. Management realized that the optimal product mix, taking setup costs into account, might be different from the one recommended in part (b). Formulate a mixed- integer linear program that takes setup costs into account. Management also stated that we should not consider making more than 140 units of product 1, 155 units of product 2, or 160 units of product 3. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300) If the coefficient of a constraint is "1", enter "1" in the answer box. Enter "0" if a coefficient or a RHS value is zero. Here introduce a 0-1 variable y i that is one if any quantity of product i is produced and zero otherwise. Max 25 P1+ 27 P 2+1 29 P 31+ -350 y 1 + -570 y 2 + -620 y 3 s.t. 3 P21+ 2 P3 $ 450 1.5 P1+ 2 P11+ 1 P21+ 2.50 P31 350 0.25 P1+ 0.25 P21+ 0.25 P3 V 50 1 P1 + o X y 1 0 1 P2 0 X y 2 V 0 1 P3 0 X Y 33 0 P1, P2, P3 2 0; y 1, y 2, Y 3 = 0,1 e. Solve the mixed-integer linear program formulated in part (d). How much of each product should be produced, and what is the projected total profit contribution? Compare this profit contribution to that obtained in part (c). Enter "O" if your answer is zero. P1 = 100 P2 = 100 P 3 = 0 Profit = $ 4,426 x The profit is increased by $ 436 X