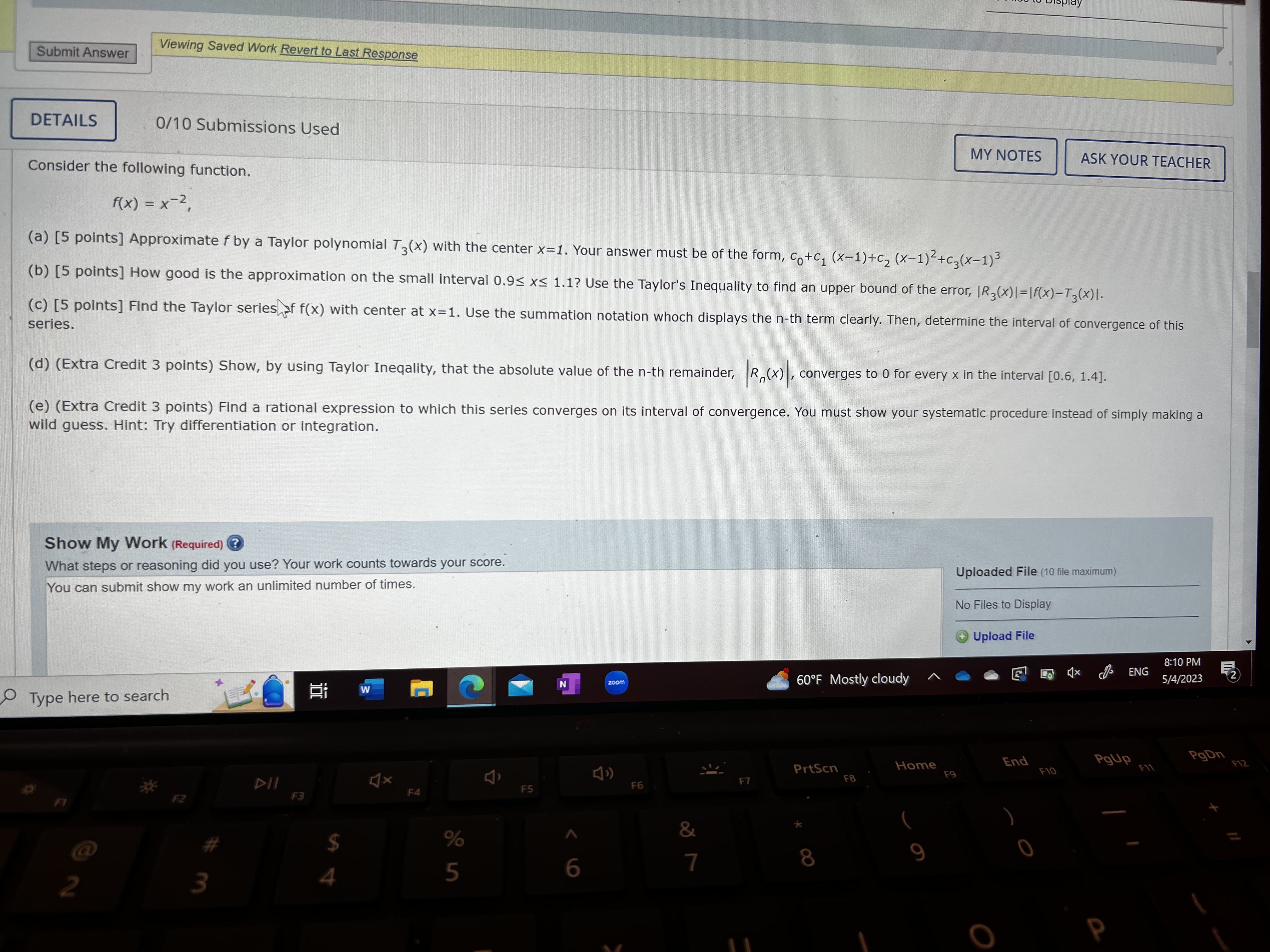
Question: Please help Submit Answer Viewing Saved Work Revert to Last Response DETAILS 0/10 Submissions Used MY NOTES ASK YOUR TEACHER Consider the following function. f
Please help
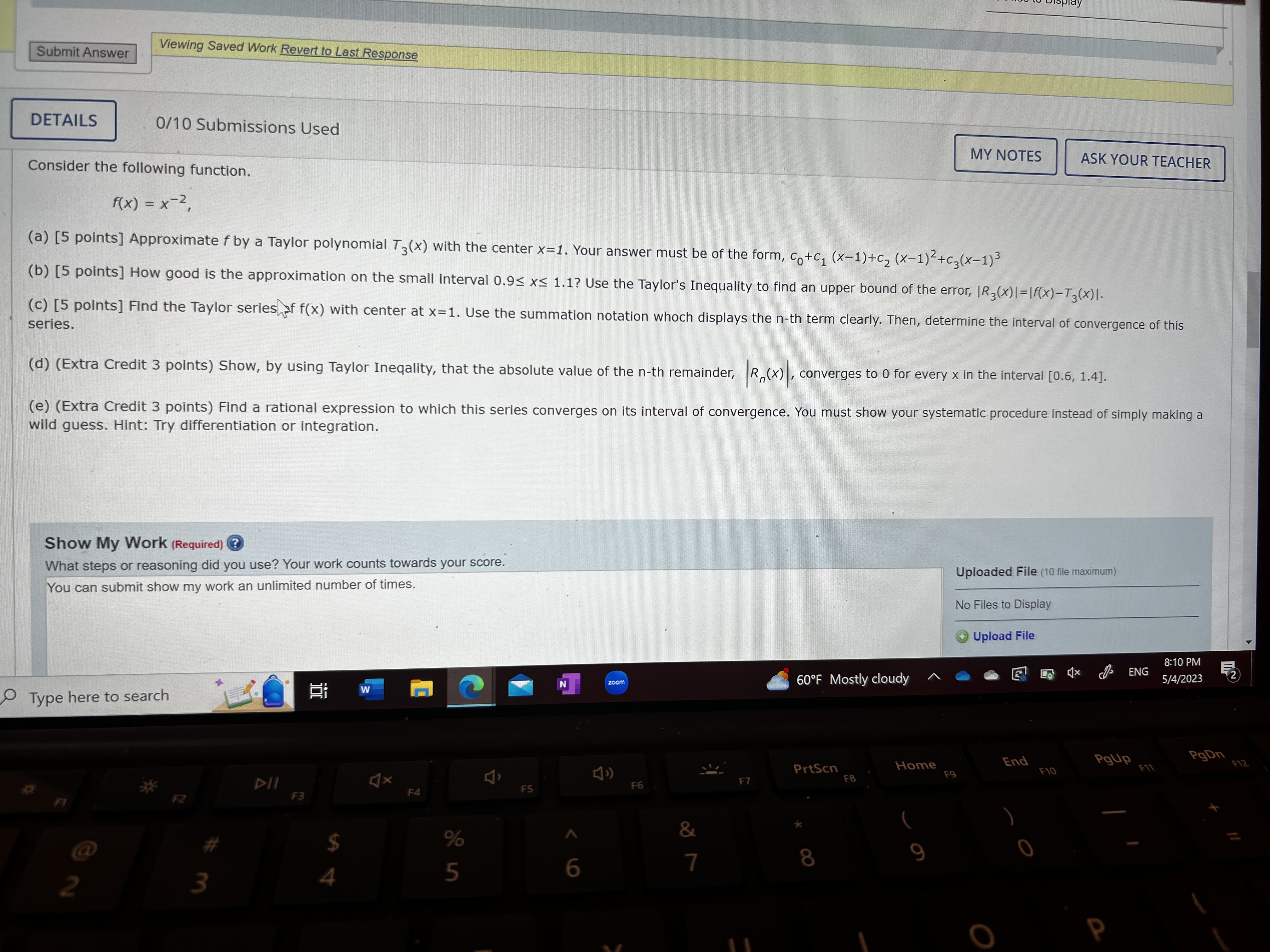
Submit Answer Viewing Saved Work Revert to Last Response DETAILS 0/10 Submissions Used MY NOTES ASK YOUR TEACHER Consider the following function. f ( x ) = x-2 (a) [5 points] Approximate f by a Taylor polynomial T3(x) with the center x=1. Your answer must be of the form, Co+c, (x-1)+c2 (x-1)2+C3(X-1)3 (b) [5 points] How good is the approximation on the small interval 0.9s xS 1.1? Use the Taylor's Inequality to find an upper bound of the error, IR,(x) |=If(x)-T3(x)1. (c) [5 points] Find the Taylor series of f(x) with center at x=1. Use the summation notation whoch displays the n-th term clearly. Then, determine the interval of convergence of this series. (d) (Extra Credit 3 points) Show, by using Taylor Ineqality, that the absolute value of the n-th remainder, R, (x) , converges to 0 for every x in the interval [0.6, 1.4]. (e) (Extra Credit 3 points) Find a rational expression to which this series converges on its interval of convergence. You must show your systematic procedure instead of simply making a wild guess. Hint: Try differentiation or integration. Show My Work (Required) ? Uploaded File (10 file maximum) What steps or reasoning did you use? Your work counts towards your score. You can submit show my work an unlimited number of times. No Files to Display +Upload File 8:10 PM ENG 60OF Mostly cloudy 5/4/2023 W N zoom Type here to search PgDn Home End PgUp F12 F11 PrtSen F9 F 10 F7 F8 DII X F6 F5 F4 F2 F3 % A O @ 4 5 2 3 D
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


