Please help

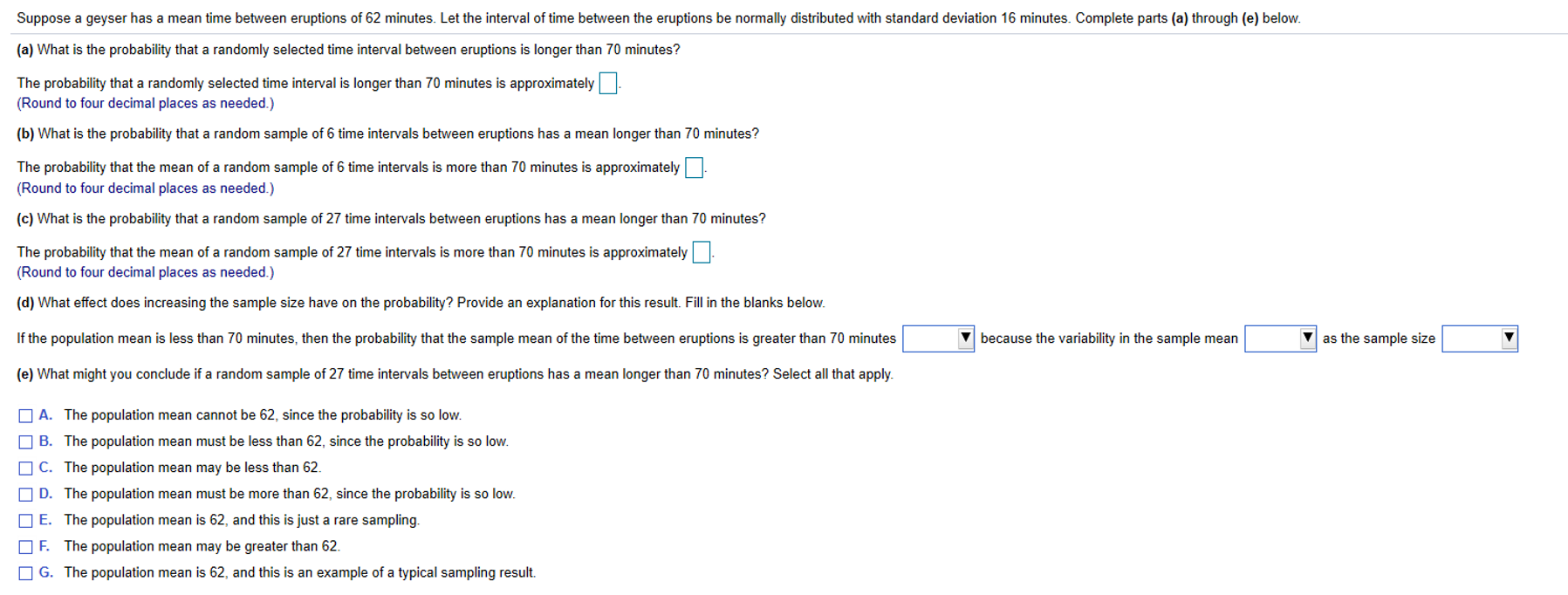
Suppose a geyser has a mean time between eruptions of 62 minutes. Let the interval of time between the eruptions be normally distributed with standard deviation 16 minutes. Complete parts (a) through (e) below. (a) What is the probability that a randomly selected time interval between eruptions is longer than 70 minutes? The probability that a randomly selected time interval is longer than 70 minutes is approximately]. (Round to four decimal places as needed.) (b) What is the probability that a random sample of 6 time intervals between eruptions has a mean longer than 70 minutes? The probability that the mean of a random sample of 6 time intervals is more than 70 minutes is approximately. (Round to four decimal places as needed.) (c) What is the probability that a random sample of 27 time intervals between eruptions has a mean longer than 70 minutes? The probability that the mean of a random sample of 27 time intervals is more than 70 minutes is approximately (Round to four decimal places as needed.) (d) What effect does increasing the sample size have on the probability? Provide an explanation for this result. Fill in the blanks below. If the population mean is less than 70 minutes, then the probability that the sample mean of the time between eruptions is greater than 70 minutes because the variability in the sample mean V as the sample size (e) What might you conclude if a random sample of 27 time intervals between eruptions has a mean longer than 70 minutes? Select all that apply. A. The population mean cannot be 62, since the probability is so low. B. The population mean must be less than 62, since the probability is so low. C. The population mean may be less than 62. D. The population mean must be more than 62, since the probability is so low. E. The population mean is 62, and this is just a rare sampling. F. The population mean may be greater than 62 G. The population mean is 62, and this is an example of a typical sampling result