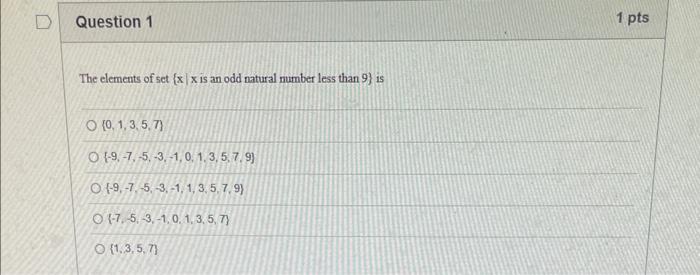
Question: please help The elements of set {xx is an odd natural number less than 9} is {0,1,3,5,7} {9,7,5,3,1,0,1,3,5,7,9} {9,7,5,3,1,1,3,5,7,9} {7,5,3,1,0,1,3,5,7} {1,3,5,7} Statement OEQ is True


![f(x)=x3 f(x)=(x2+1)/(x2+2) Let A=[aij] be a mm matrix, B=[aiji] be a mm](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66f450527a58e_37766f45051ee311.jpg)
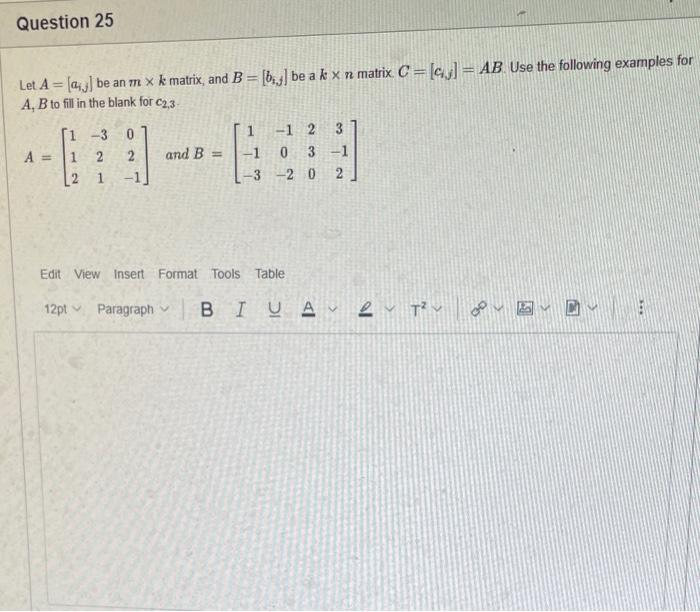
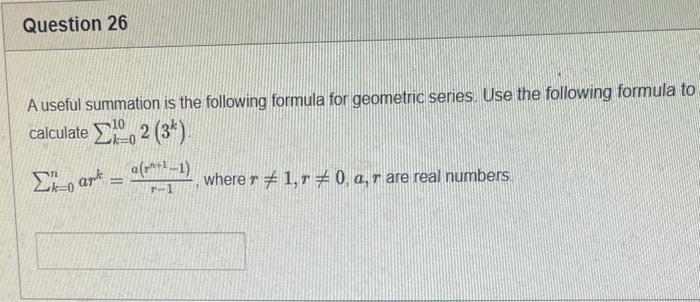
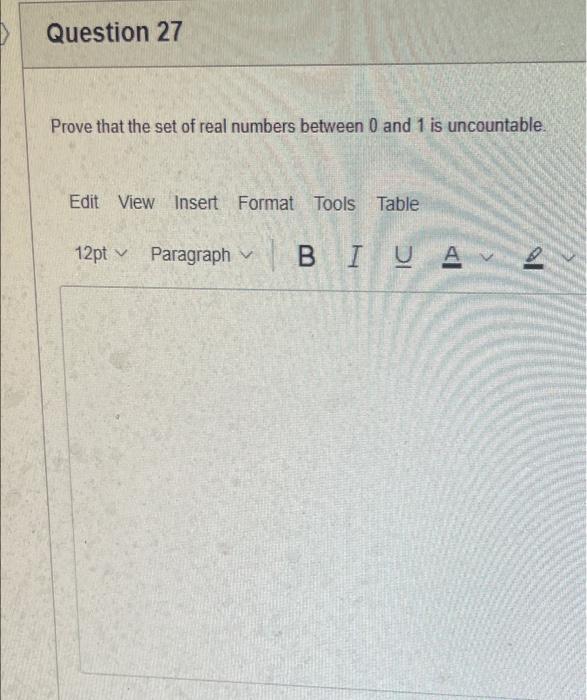
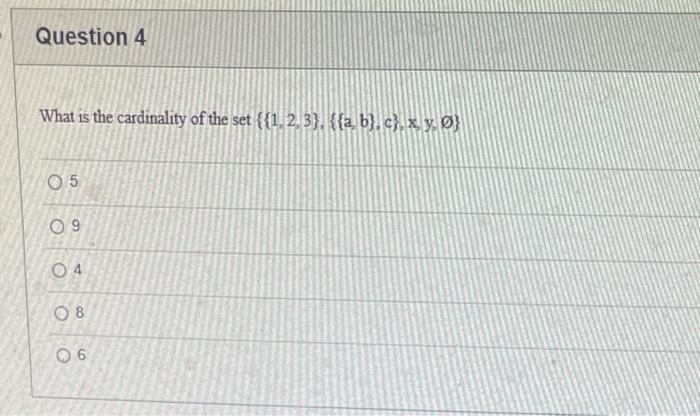
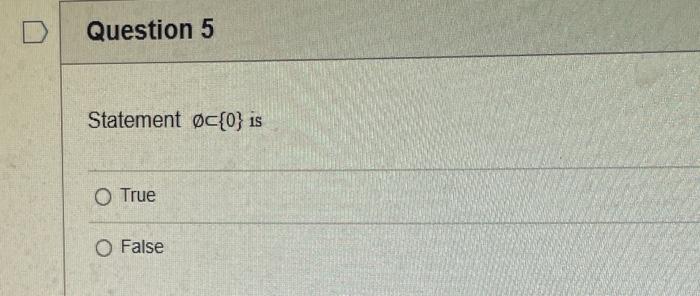
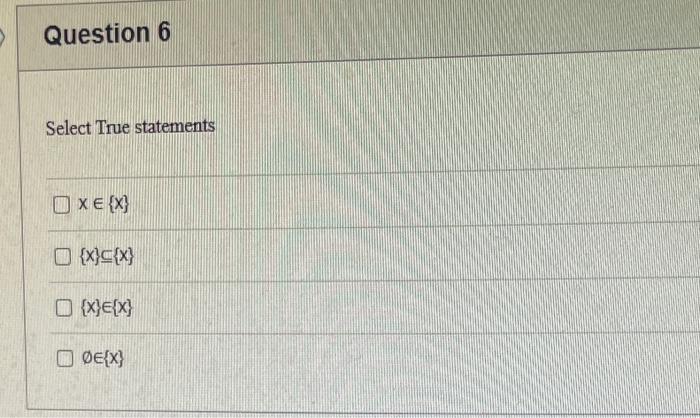
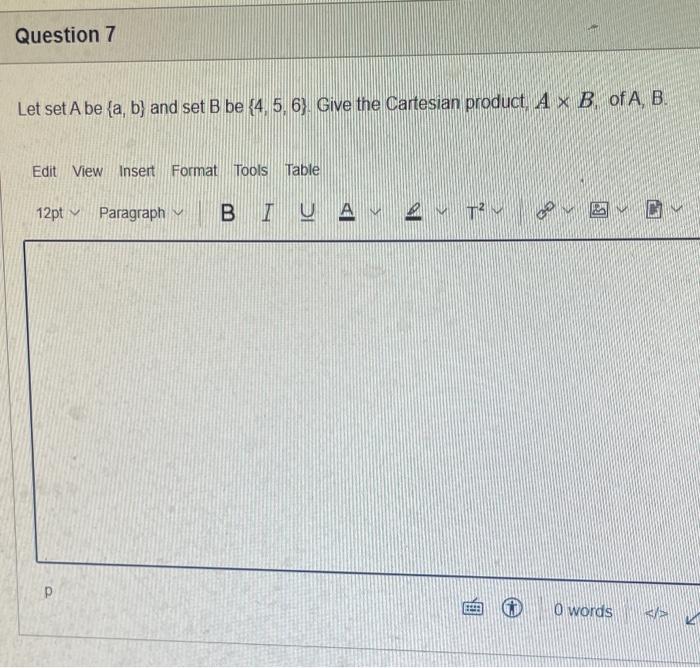
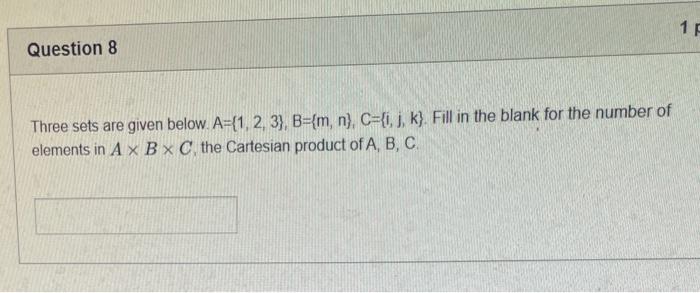
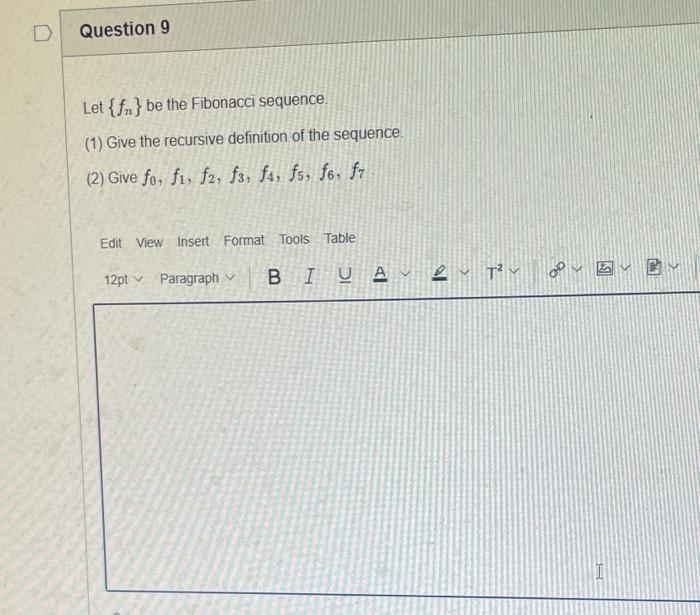
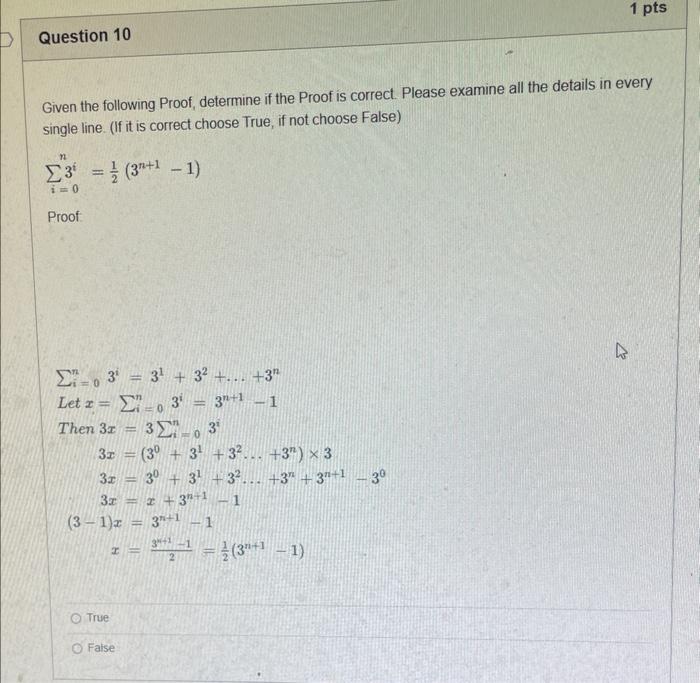
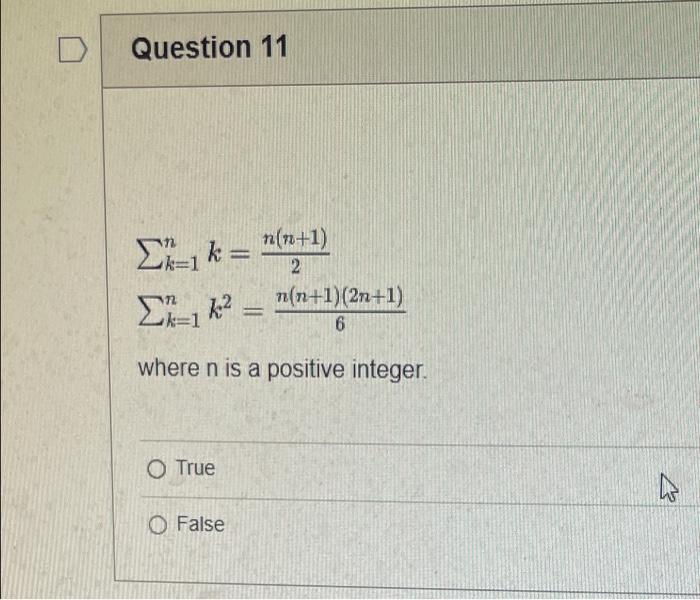
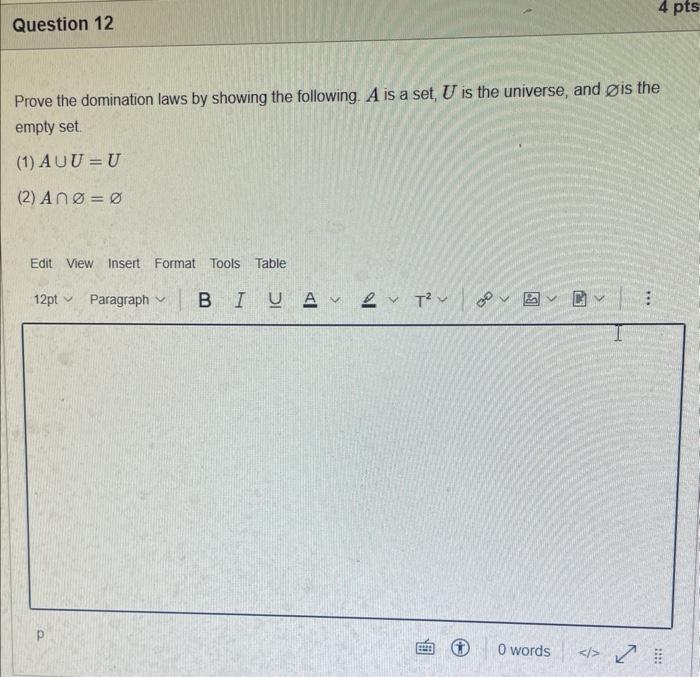
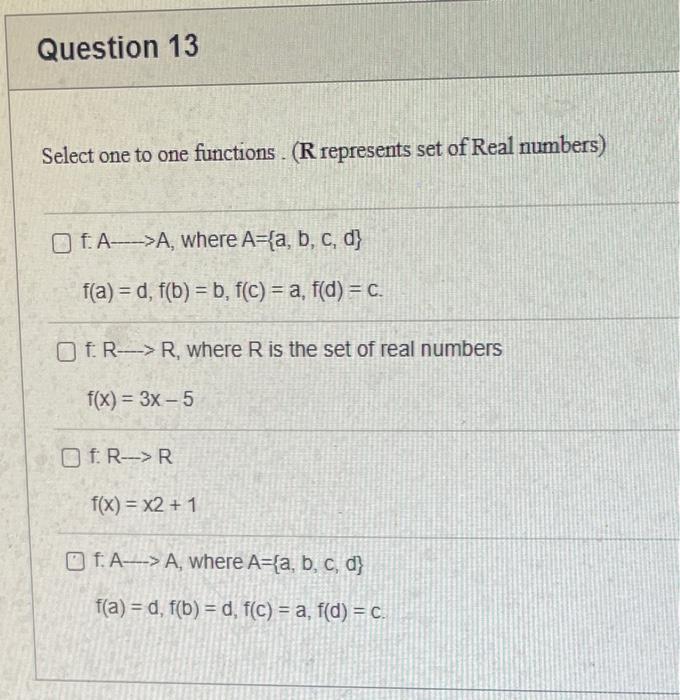
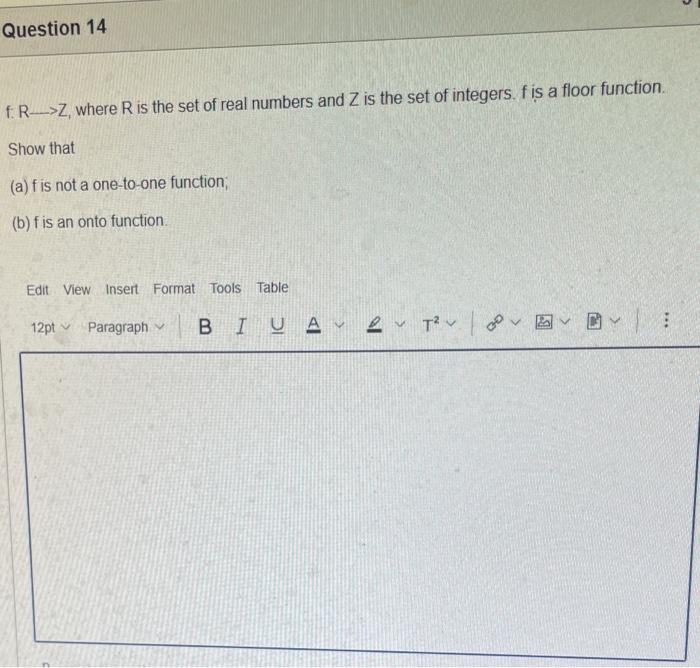
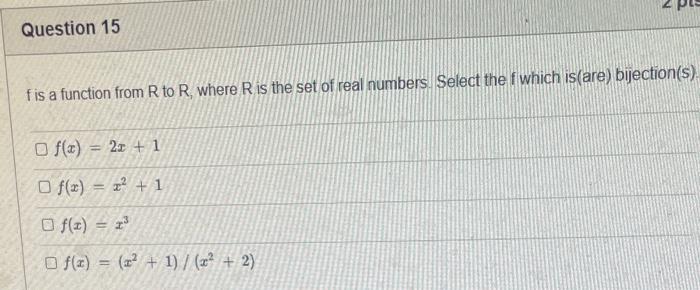
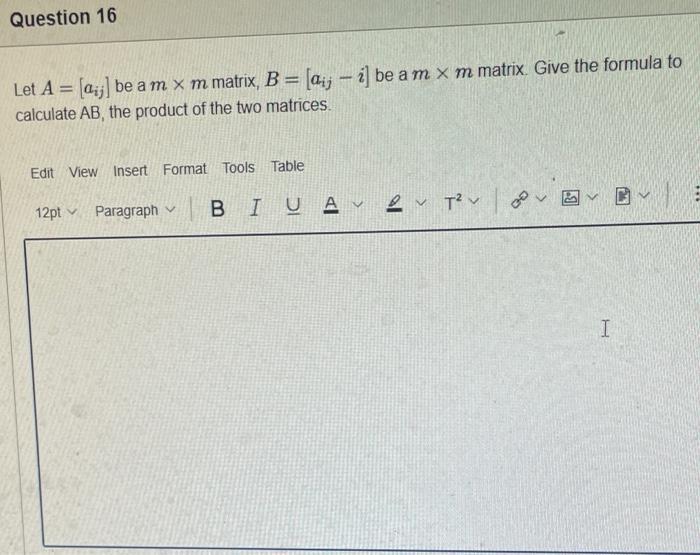
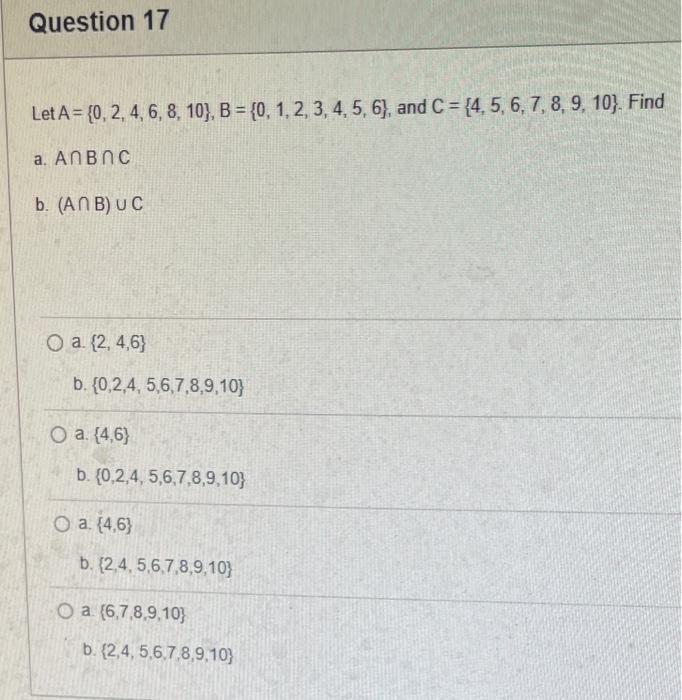
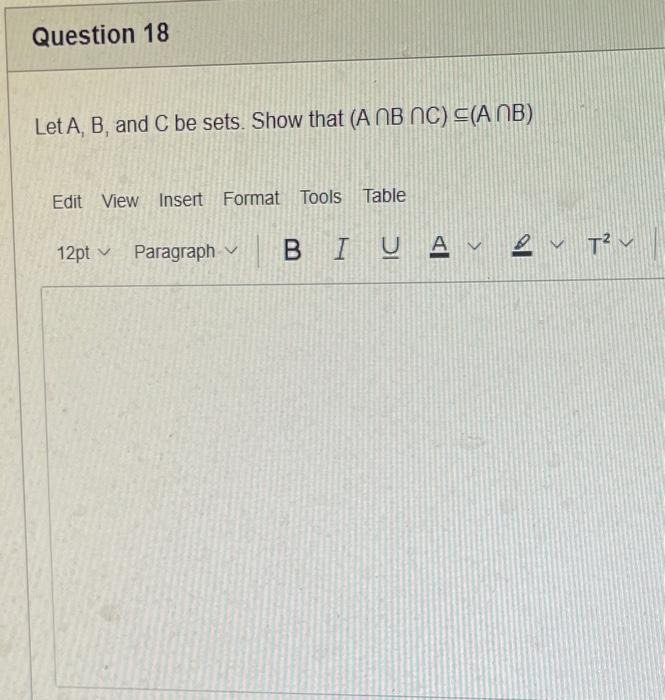
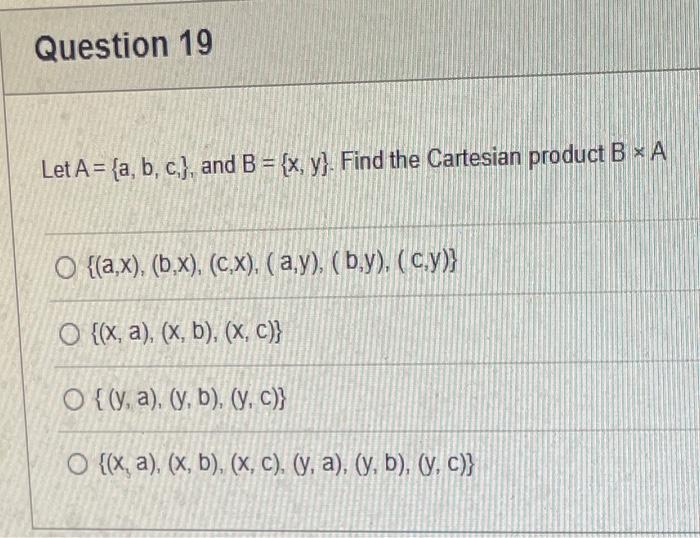
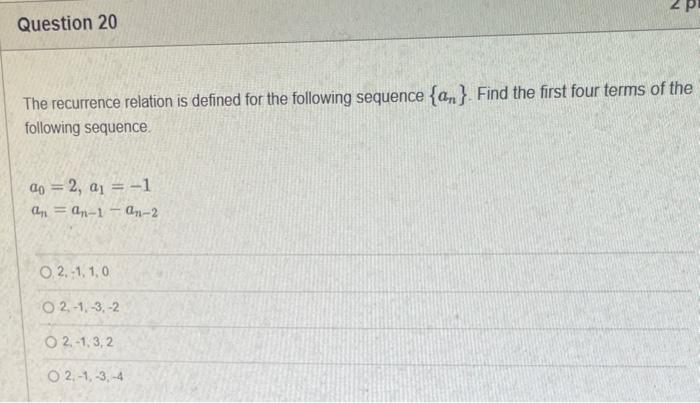
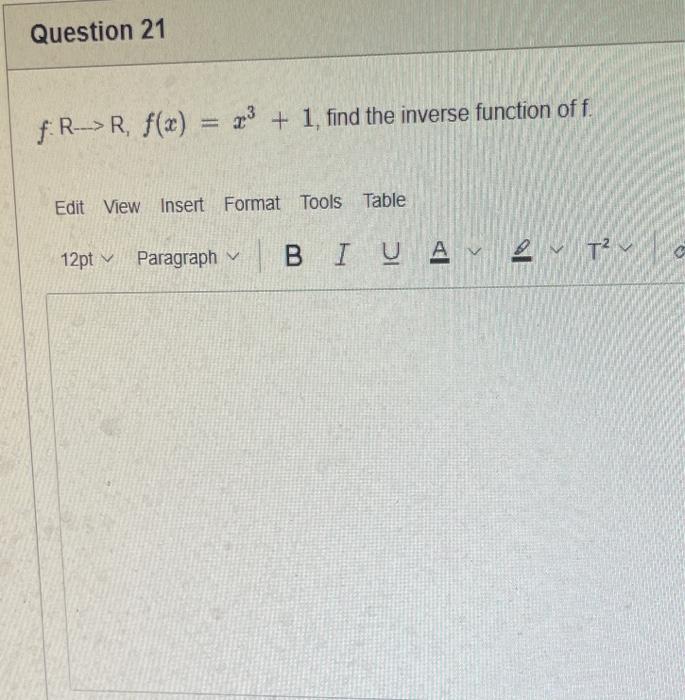
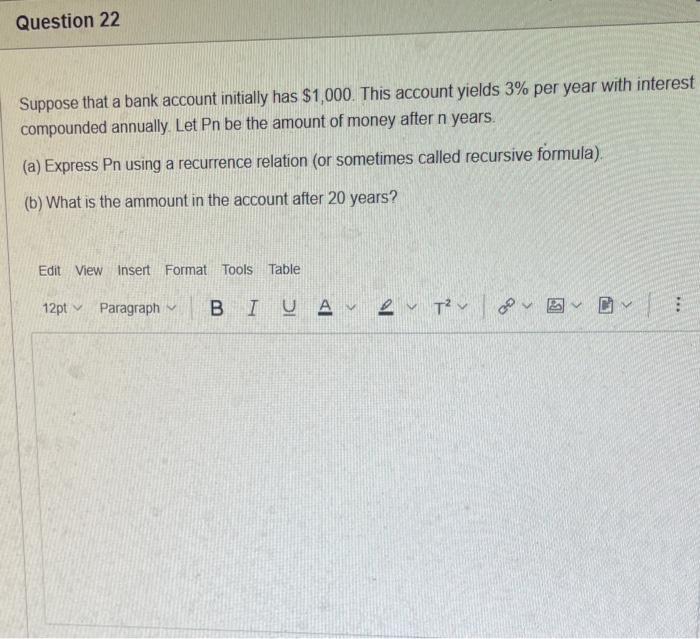
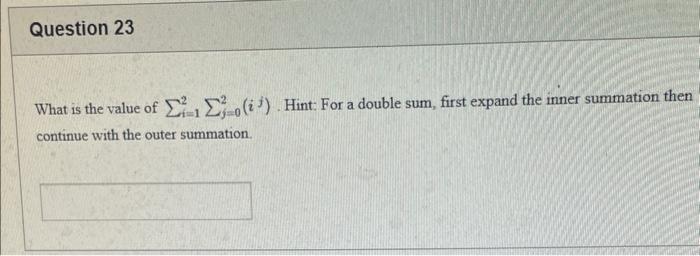
The elements of set {xx is an odd natural number less than 9} is {0,1,3,5,7} {9,7,5,3,1,0,1,3,5,7,9} {9,7,5,3,1,1,3,5,7,9} {7,5,3,1,0,1,3,5,7} {1,3,5,7} Statement OEQ is True False 1 pts Question 3 {0}{0} True False What is the cardinality of the set {{1,2,3},{{a,b},c},x,y,} 5 9 4 8 6 Statement {0} is True False Select True statements x{X} {x}{x} {x}{x} {X} Let set A be {a,b} and set B be {4,5,6}. Give the Cartesian product, AB, of A,B. Three sets are given below. A={1,2,3},B={m,n},C={i,j,k}. Fill in the blank for the number of elements in ABC, the Cartesian product of A,B,C. Let {fn} be the Fibonacci sequence. (1) Give the recursive definition of the sequence. (2) Give f0,f1,f2,f3,f4,f5,f6,f7. Given the following Proof, determine if the Proof is correct. Please examine all the details in every single line. (If it is correct choose True, if not choose False) i=0n3i=21(3n+11) Proof: i=0n3i=31+32++3nLetx=in=3i=3n+11Then3x=3i=0n3i3x=(30+31+32+3n)33x=30+31+32+3n+3n+1303x=x+3n+11(31)x=3n+11x=23n+11=21(3n+11) True Faise Question 11 k=1nk=2n(n+1)k=1nk2=6n(n+1)(2n+1) where n is a positive integer. True False Prove the domination laws by showing the following. A is a set, U is the universe, and is the empty set. (1) AU=U (2) A= Select one to one functions. ( R represents set of Real numbers) f.AA, where A={a,b,c,d} f(a)=d,f(b)=b,f(c)=a,f(d)=c f:RR, where R is the set of real numbers f(x)=3x5 f:RR f(x)=x2+1 f:AA, where A={a,b,c,d} f(a)=d,f(b)=d,f(c)=a,f(d)=c f:RZ, where R is the set of real numbers and Z is the set of integers. f is a floor function. Show that (a) f is not a one-to-one function; (b) f is an onto function. f is a function from R to R, where R is the set of real numbers. Select the f which is(are) bijection(S) f(x)=2x+1 f(x)=x2+1 f(x)=x3 f(x)=(x2+1)/(x2+2) Let A=[aij] be a mm matrix, B=[aiji] be a mm matrix. Give the formula to calculate AB, the product of the two matrices Let A={0,2,4,6,8,10},B={0,1,2,3,4,5,6}, and C={4,5,6,7,8,9,10}. Find a. ABC b. (AB)C a. {2,4,6} b. {0,2,4,5,6,7,8,9,10} a. {4,6} b. {0,2,4,5,6,7,8,9,10} a. {4,6} b. {2,4,5,6,7,8,9,10} a {6,7,8,9,10} b. {2,4,5,6,7,8,9,10} Let A,B, and C be sets. Show that (ABC)(AB) Let A={a,b,c,},andB={x,y}. Find the Cartesian product BA {(a,x),(b,x),(c,x),(a,y),(b,y),(c,y)} {(x,a),(x,b),(x,c)} {(y,a),(y,b),(y,c)} {(x,a),(x,b),(x,c),(y,a),(y,b),(y,c)} The recurrence relation is defined for the following sequence {an}. Find the first four terms of the following sequence. a0=2,a1=1an=an1an2 2. 1,1,0 2, 1,3,2 2. 1,3,2 2,1,3,4 f:RR,f(x)=x3+1, find the inverse function of f. Suppose that a bank account initially has $1,000. This account yields 3% per year with interest compounded annually. Let Pn be the amount of money after n years. (a) Express Pn using a recurrence relation (or sometimes called recursive formula). (b) What is the ammount in the account after 20 years? What is the value of i=12j=02(ij). Hint: For a double sum, first expand the inner summation then continue with the outer summation. j=08(2j+12j)511531469369 Let A=[ai,j] be an mk matrix, and B=[bi,j] be a kn matrix C=[ci,j]=AB. Use the following examples for A,B to fill in the blank for c2,3 A=112321021andB=113102230312 A useful summation is the following formula for geometric series. Use the following formula to calculate k=0102(3k) k=0nark=r1a(rn+11), where r=1,r=0,a,r are real numbers Prove that the set of real numbers between 0 and 1 is uncountable. Let A,B be two sets. Let P(A) and P(B) denote the power set of A and B respectively. Show that if P(A)P(B), then AB. The elements of set {xx is an odd natural number less than 9} is {0,1,3,5,7} {9,7,5,3,1,0,1,3,5,7,9} {9,7,5,3,1,1,3,5,7,9} {7,5,3,1,0,1,3,5,7} {1,3,5,7} Statement OEQ is True False 1 pts Question 3 {0}{0} True False What is the cardinality of the set {{1,2,3},{{a,b},c},x,y,} 5 9 4 8 6 Statement {0} is True False Select True statements x{X} {x}{x} {x}{x} {X} Let set A be {a,b} and set B be {4,5,6}. Give the Cartesian product, AB, of A,B. Three sets are given below. A={1,2,3},B={m,n},C={i,j,k}. Fill in the blank for the number of elements in ABC, the Cartesian product of A,B,C. Let {fn} be the Fibonacci sequence. (1) Give the recursive definition of the sequence. (2) Give f0,f1,f2,f3,f4,f5,f6,f7. Given the following Proof, determine if the Proof is correct. Please examine all the details in every single line. (If it is correct choose True, if not choose False) i=0n3i=21(3n+11) Proof: i=0n3i=31+32++3nLetx=in=3i=3n+11Then3x=3i=0n3i3x=(30+31+32+3n)33x=30+31+32+3n+3n+1303x=x+3n+11(31)x=3n+11x=23n+11=21(3n+11) True Faise Question 11 k=1nk=2n(n+1)k=1nk2=6n(n+1)(2n+1) where n is a positive integer. True False Prove the domination laws by showing the following. A is a set, U is the universe, and is the empty set. (1) AU=U (2) A= Select one to one functions. ( R represents set of Real numbers) f.AA, where A={a,b,c,d} f(a)=d,f(b)=b,f(c)=a,f(d)=c f:RR, where R is the set of real numbers f(x)=3x5 f:RR f(x)=x2+1 f:AA, where A={a,b,c,d} f(a)=d,f(b)=d,f(c)=a,f(d)=c f:RZ, where R is the set of real numbers and Z is the set of integers. f is a floor function. Show that (a) f is not a one-to-one function; (b) f is an onto function. f is a function from R to R, where R is the set of real numbers. Select the f which is(are) bijection(S) f(x)=2x+1 f(x)=x2+1 f(x)=x3 f(x)=(x2+1)/(x2+2) Let A=[aij] be a mm matrix, B=[aiji] be a mm matrix. Give the formula to calculate AB, the product of the two matrices Let A={0,2,4,6,8,10},B={0,1,2,3,4,5,6}, and C={4,5,6,7,8,9,10}. Find a. ABC b. (AB)C a. {2,4,6} b. {0,2,4,5,6,7,8,9,10} a. {4,6} b. {0,2,4,5,6,7,8,9,10} a. {4,6} b. {2,4,5,6,7,8,9,10} a {6,7,8,9,10} b. {2,4,5,6,7,8,9,10} Let A,B, and C be sets. Show that (ABC)(AB) Let A={a,b,c,},andB={x,y}. Find the Cartesian product BA {(a,x),(b,x),(c,x),(a,y),(b,y),(c,y)} {(x,a),(x,b),(x,c)} {(y,a),(y,b),(y,c)} {(x,a),(x,b),(x,c),(y,a),(y,b),(y,c)} The recurrence relation is defined for the following sequence {an}. Find the first four terms of the following sequence. a0=2,a1=1an=an1an2 2. 1,1,0 2, 1,3,2 2. 1,3,2 2,1,3,4 f:RR,f(x)=x3+1, find the inverse function of f. Suppose that a bank account initially has $1,000. This account yields 3% per year with interest compounded annually. Let Pn be the amount of money after n years. (a) Express Pn using a recurrence relation (or sometimes called recursive formula). (b) What is the ammount in the account after 20 years? What is the value of i=12j=02(ij). Hint: For a double sum, first expand the inner summation then continue with the outer summation. j=08(2j+12j)511531469369 Let A=[ai,j] be an mk matrix, and B=[bi,j] be a kn matrix C=[ci,j]=AB. Use the following examples for A,B to fill in the blank for c2,3 A=112321021andB=113102230312 A useful summation is the following formula for geometric series. Use the following formula to calculate k=0102(3k) k=0nark=r1a(rn+11), where r=1,r=0,a,r are real numbers Prove that the set of real numbers between 0 and 1 is uncountable. Let A,B be two sets. Let P(A) and P(B) denote the power set of A and B respectively. Show that if P(A)P(B), then AB
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


