Please help with 1.71

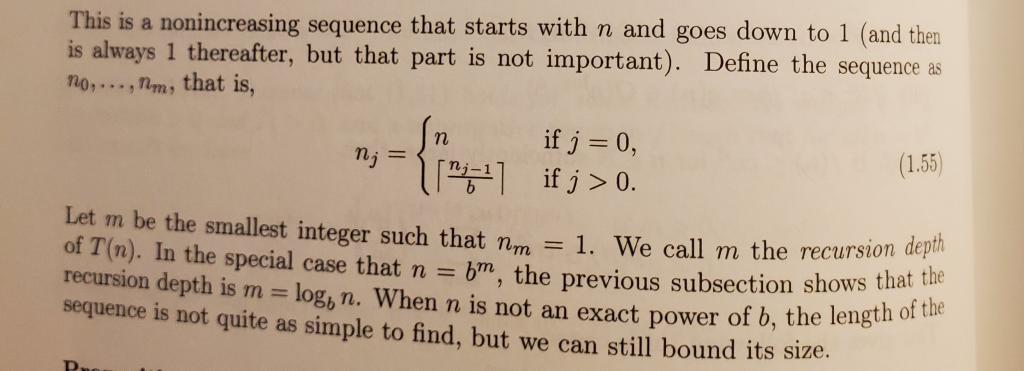
1.67. Find an exact closed-form formula for T in each of the following recursions when n=2m for mZ+: (i) T(n)=8T(2n)+n. (ii) T(n)=3T(2n)+n. (iii) T(n)=3T(2n)+n3. 1.68. Prove that the recurrence T(n)=3T([4n)+nlogn,n2, with T(1)=T1>0, satisfies T(n)O(nlogn). 1.69. Assume that T(n) satisfies the recurrence (1.45) for n=bm for mN. Generalize Theorem 1.10.2(ii) by proving the following theorem: If d=logba and f(n)O(nd(logn)), then T(n)O(nd(logn)+1). Hint: Show that T(n)O(ndm+1) and then use the fact that m=logbn. 1.70. Show that the sequence (1.55) satisfies bknnk for each k{0,1,2,,m}. In particular, bmnnm=1. 1.71. Prove that recursion depth m, given by the sequence (1.55), is bounded below by logbn, that is, mlogbn. This is a nonincreasing sequence that starts with n and goes down to 1 (and then is always 1 thereafter, but that part is not important). Define the sequence as n0,,nm, that is nj={nbnj1ifj=0ifj>0 Let m be the smallest integer such that nm=1. We call m the recursion depth of T(n). In the special case that n=bm, the previous subsection shows that the recursion depth is m=logbn. When n is not an exact power of b, the length of the sequence is not quite as simple to find, but we can still bound its size. 1.67. Find an exact closed-form formula for T in each of the following recursions when n=2m for mZ+: (i) T(n)=8T(2n)+n. (ii) T(n)=3T(2n)+n. (iii) T(n)=3T(2n)+n3. 1.68. Prove that the recurrence T(n)=3T([4n)+nlogn,n2, with T(1)=T1>0, satisfies T(n)O(nlogn). 1.69. Assume that T(n) satisfies the recurrence (1.45) for n=bm for mN. Generalize Theorem 1.10.2(ii) by proving the following theorem: If d=logba and f(n)O(nd(logn)), then T(n)O(nd(logn)+1). Hint: Show that T(n)O(ndm+1) and then use the fact that m=logbn. 1.70. Show that the sequence (1.55) satisfies bknnk for each k{0,1,2,,m}. In particular, bmnnm=1. 1.71. Prove that recursion depth m, given by the sequence (1.55), is bounded below by logbn, that is, mlogbn. This is a nonincreasing sequence that starts with n and goes down to 1 (and then is always 1 thereafter, but that part is not important). Define the sequence as n0,,nm, that is nj={nbnj1ifj=0ifj>0 Let m be the smallest integer such that nm=1. We call m the recursion depth of T(n). In the special case that n=bm, the previous subsection shows that the recursion depth is m=logbn. When n is not an exact power of b, the length of the sequence is not quite as simple to find, but we can still bound its size