please help with how I can get the numbers painted in red and also I cannot get the number painted in green, please also write down the formula thanks a lot

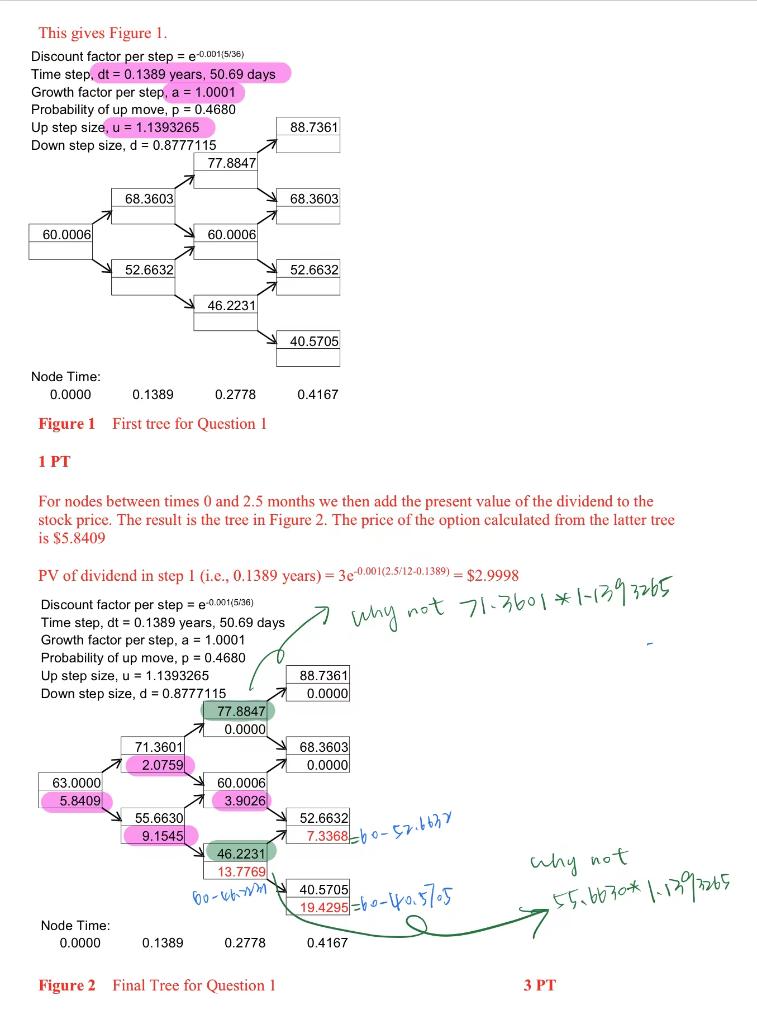
QUESTION 4 [4 +2+2 = 8 MARKS] Gloria Delgado owns 500 shares of Rio Tinto stock, listed on Nasdaq. Today is November 12th, 2020 and the stock, currently trading at S63, is already down since the time Gloria purchased it. Fearing further declines, she decides to hedge with Rio Tinto put options with a strike of S60 and expiring in April 2021 (a 5-month maturity). As a financial intermediary, you are willing to write the options to Gloria and need to price them. The options are American style. To this end, you look up the implied volatility from some traded options on Rio Tinto and sees that it is at 35% per annum. You also check Rio Tinto stock and see that the company will pay a dividend of $3 in 2.5 months from today and a dividend of $5 in 6.5 months from today. The Reserve Bank of Australia (RBA) has recently cut the risk-free rate of interest to 0.10% p.a. (continuously compounded) a) Use a three-step binomial tree to calculate the option price. Round u and d to 7 decimal digits so that the tree recombines. For all other calculations, round to 4 decimal digits at each step. We first build a tree for starting at S0 = 63- PV(3) = 63-3*exp(-0.0010*2.5/12) = $60.0006 using K=60; rf 0.10%; sigma = 35%; T = 5/12; 16 This gives Figure 1. Discount factor per step = e-0.001(5/36) Time step, dt = 0.1389 years, 50.69 days Growth factor per step, a = 1.0001 Probability of up move, p = 0.4680 Up step size, u = 1.1393265 Down step size, d = 0.8777115 88.7361 77.8847 7 68.3603 68.3603 60.0006 60.0006 52.6632 52.6632 46.2231 40.5705 Node Time: 0.0000 0.1389 0.2778 0.4167 Figure 1 First tree for Question 1 1 PT For nodes between times 0 and 2.5 months we then add the present value of the dividend to the stock price. The result is the tree in Figure 2. The price of the option calculated from the latter tree is $5.8409 PV of dividend in step 1 (i.e., 0.1389 years) = 3e-0.001(2.5/12-0.1389) = $2.9998 Discount factor per step=e-0.001(5/36) Time step, dt = 0.1389 years, 50.69 days 7 why not 71-3601*1-1393265 Growth factor per step, a = 1.0001 Probability of up move, p = 0.4680 Up step size, u = 1.1393265 88.7361 Down step size, d = 0.8777115 0.0000 77.8847 0.0000 71.3601 68.3603 2.0759 0.0000 63.0000 60.0006 5.8409 3.9026 55.6630 52.6632 9.1545 77.3368-0-52.6627 46.2231 13.7769 40.5705 why not 55.6630*1.1392265 19.4295-60-0.575 Node Time: 0.0000 0.1389 0.2778 0.4167 Figure 2 Final Tree for Question 1 3 PT 60-66 QUESTION 4 [4 +2+2 = 8 MARKS] Gloria Delgado owns 500 shares of Rio Tinto stock, listed on Nasdaq. Today is November 12th, 2020 and the stock, currently trading at S63, is already down since the time Gloria purchased it. Fearing further declines, she decides to hedge with Rio Tinto put options with a strike of S60 and expiring in April 2021 (a 5-month maturity). As a financial intermediary, you are willing to write the options to Gloria and need to price them. The options are American style. To this end, you look up the implied volatility from some traded options on Rio Tinto and sees that it is at 35% per annum. You also check Rio Tinto stock and see that the company will pay a dividend of $3 in 2.5 months from today and a dividend of $5 in 6.5 months from today. The Reserve Bank of Australia (RBA) has recently cut the risk-free rate of interest to 0.10% p.a. (continuously compounded) a) Use a three-step binomial tree to calculate the option price. Round u and d to 7 decimal digits so that the tree recombines. For all other calculations, round to 4 decimal digits at each step. We first build a tree for starting at S0 = 63- PV(3) = 63-3*exp(-0.0010*2.5/12) = $60.0006 using K=60; rf 0.10%; sigma = 35%; T = 5/12; 16 This gives Figure 1. Discount factor per step = e-0.001(5/36) Time step, dt = 0.1389 years, 50.69 days Growth factor per step, a = 1.0001 Probability of up move, p = 0.4680 Up step size, u = 1.1393265 Down step size, d = 0.8777115 88.7361 77.8847 7 68.3603 68.3603 60.0006 60.0006 52.6632 52.6632 46.2231 40.5705 Node Time: 0.0000 0.1389 0.2778 0.4167 Figure 1 First tree for Question 1 1 PT For nodes between times 0 and 2.5 months we then add the present value of the dividend to the stock price. The result is the tree in Figure 2. The price of the option calculated from the latter tree is $5.8409 PV of dividend in step 1 (i.e., 0.1389 years) = 3e-0.001(2.5/12-0.1389) = $2.9998 Discount factor per step=e-0.001(5/36) Time step, dt = 0.1389 years, 50.69 days 7 why not 71-3601*1-1393265 Growth factor per step, a = 1.0001 Probability of up move, p = 0.4680 Up step size, u = 1.1393265 88.7361 Down step size, d = 0.8777115 0.0000 77.8847 0.0000 71.3601 68.3603 2.0759 0.0000 63.0000 60.0006 5.8409 3.9026 55.6630 52.6632 9.1545 77.3368-0-52.6627 46.2231 13.7769 40.5705 why not 55.6630*1.1392265 19.4295-60-0.575 Node Time: 0.0000 0.1389 0.2778 0.4167 Figure 2 Final Tree for Question 1 3 PT 60-66