Question: Please help with the problems below Q1 QUESTION 1 . 1 POINT Given the function of f(a) = 8x2 - 8x on the interval [0,
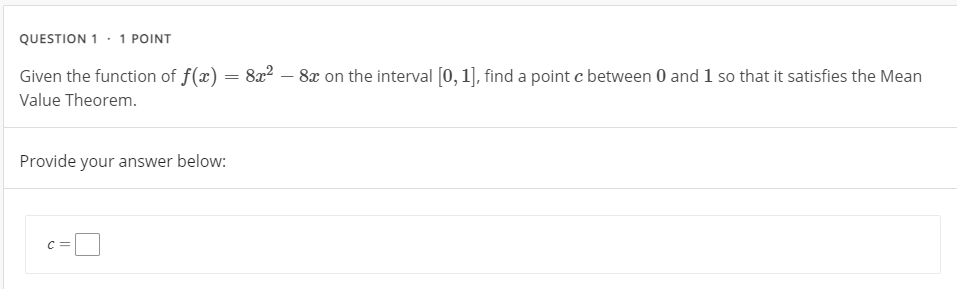

![interval [0, 1], find a point c between 0 and 1 so](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66765cd17bdcc_04166765cd16c637.jpg)


Please help with the problems below
Q1
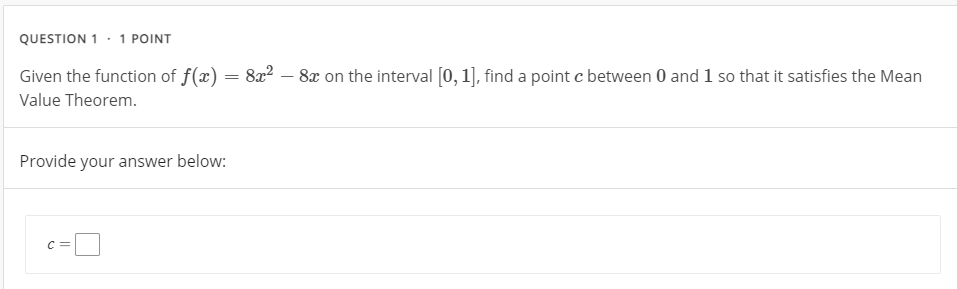




QUESTION 1 . 1 POINT Given the function of f(a) = 8x2 - 8x on the interval [0, 1], find a point c between 0 and 1 so that it satisfies the Mean Value Theorem. Provide your answer below: C=QUESTION 2 . 1 POINT A triangle has a base that is decreasing at a rate of 11 cm/s with the height being held constant. What is the rate of change of the area of the triangle if the height is 7 cm? Provide your answer below: The rate of change of the area of the triangle is cm-/s .QUESTION 3 . 1 POINT Use the First Derivative Test to find the location of all local extrema for the function given below. Enter an exact answer. If there is more than one local maxima or local minima, write each value of a separated by a comma. If a local maxima or local minima does not occur on the function, enter 0 in the appropriate box. 2023 f(z) = -2+ +1 3 Provide your answer below: . Local maxima occur at x = . Local minima occur at x =QUESTION-ll - 1 POINT Astreet light is at the top ofa pole that has a height of 15 ft . A woman 5 fl; tall walks away from the pole with a speed of 2 ft/s along a straight path. How fast is the tip of her shadow moving when she is 12 ft from the base of the pole? {Leave your answer as an exact number.) Provide your answer below: Her shadow is moving at El lls QUESTION 9 . 1 POINT Evaluate the following limit using L'Hospital's rule. lim (cos(9x)) (172 ) 1-+0 Provide your answer below: lim (cos (9x) ) x 4 0+
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


