please help with the questions

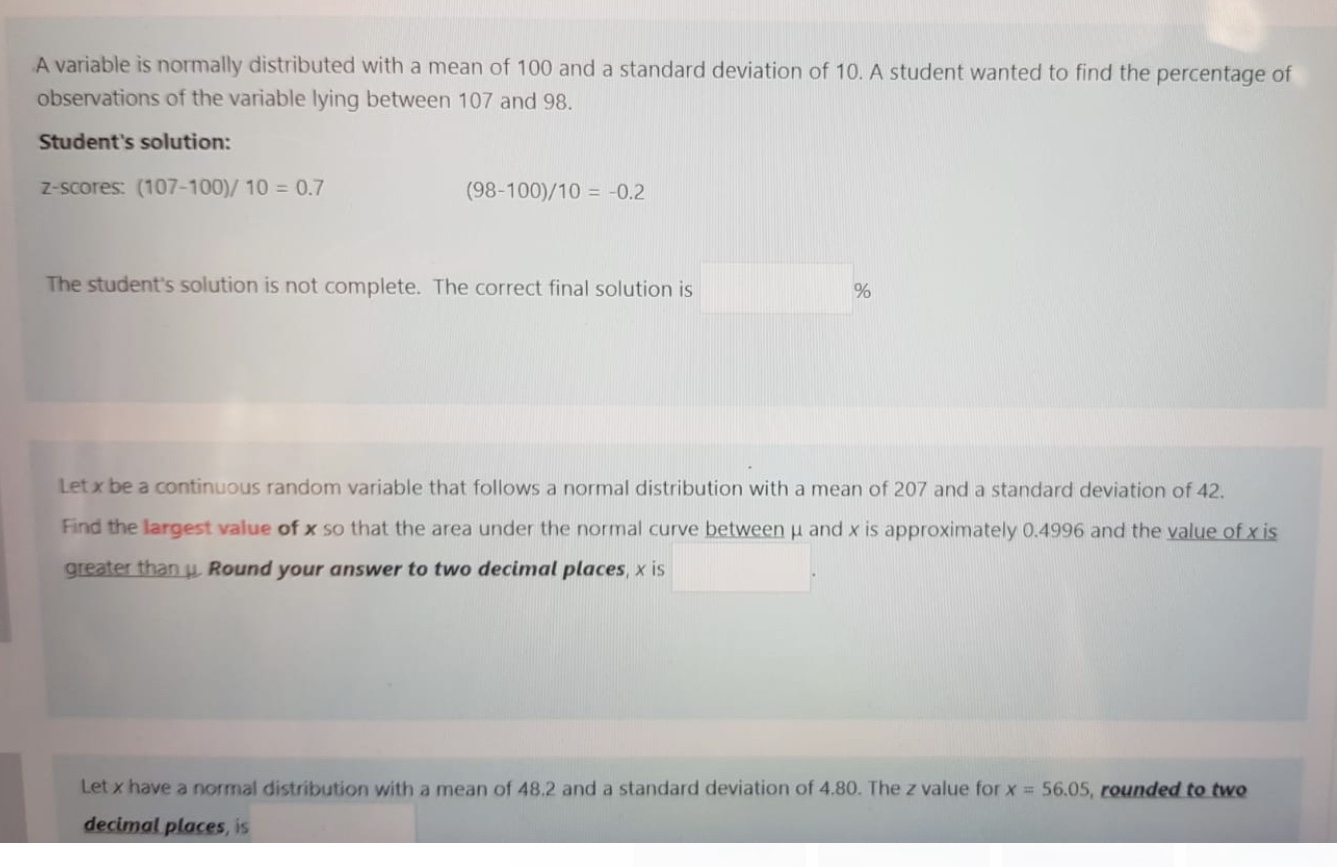
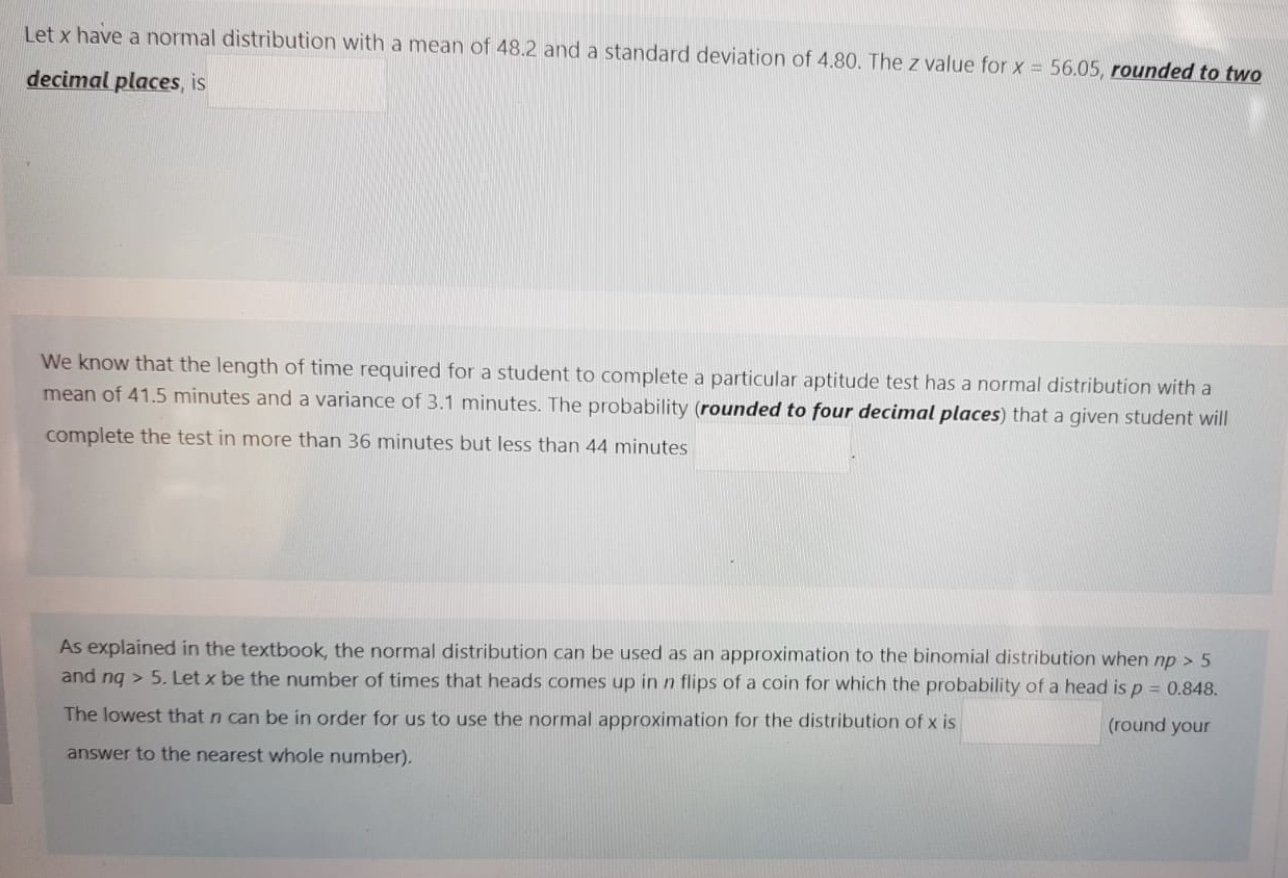
A variable is normally distributed with a mean of 100 and a standard deviation of 10. A student wanted to find the percentage of observations of the variable lying between 107 and 98. Student's solution: z-scores: (107-100)/ 10 = 0.7 (98-100)/10 = -0.2 The student's solution is not complete. The correct final solution is % Let x be a continuous random variable that follows a normal distribution with a mean of 207 and a standard deviation of 42. Find the largest value of x so that the area under the normal curve between u and x is approximately 0.4996 and the value of x is greater than u. Round your answer to two decimal places, x is Let x have a normal distribution with a mean of 48.2 and a standard deviation of 4.80. The z value for x = 56.05, rounded to two decimal places, isLet x have a normal distribution with a mean of 48.2 and a standard deviation of 4.80. The z value for x = 56.05, rounded to two decimal places, is We know that the length of time required for a student to complete a particular aptitude test has a normal distribution with a mean of 41.5 minutes and a variance of 3.1 minutes. The probability (rounded to four decimal places) that a given student will complete the test in more than 36 minutes but less than 44 minutes As explained in the textbook, the normal distribution can be used as an approximation to the binomial distribution when np > 5 and nq > 5. Let x be the number of times that heads comes up in n flips of a coin for which the probability of a head is p = 0.848. The lowest that n can be in order for us to use the normal approximation for the distribution of x is (round your answer to the nearest whole number).For a continuous random variable x, the population mean and the population standard deviation are 139 and 9, respectively. You take a simple random sample of 36 elements from this population. The mean of the sampling distribution of the sample mean is Let x be a continuous random variable that follows a normal distribution with a mean of 200 and a standard deviation of 51. Find the value of x so that the area under the normal curve to the right of x is approximately 0.3264. Rounded to two decimal places, x is