Please help with this question

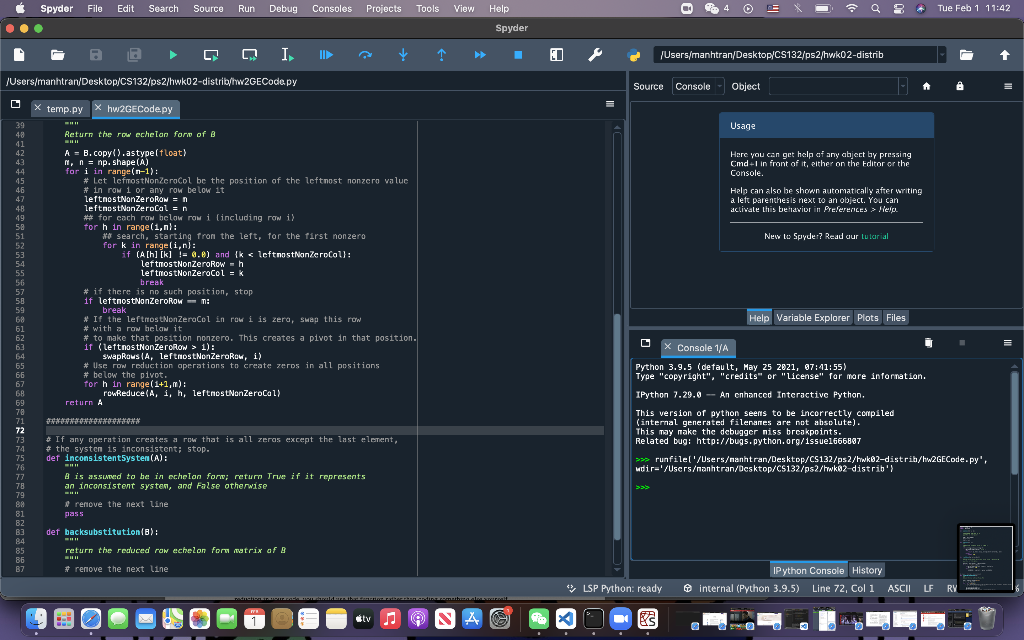
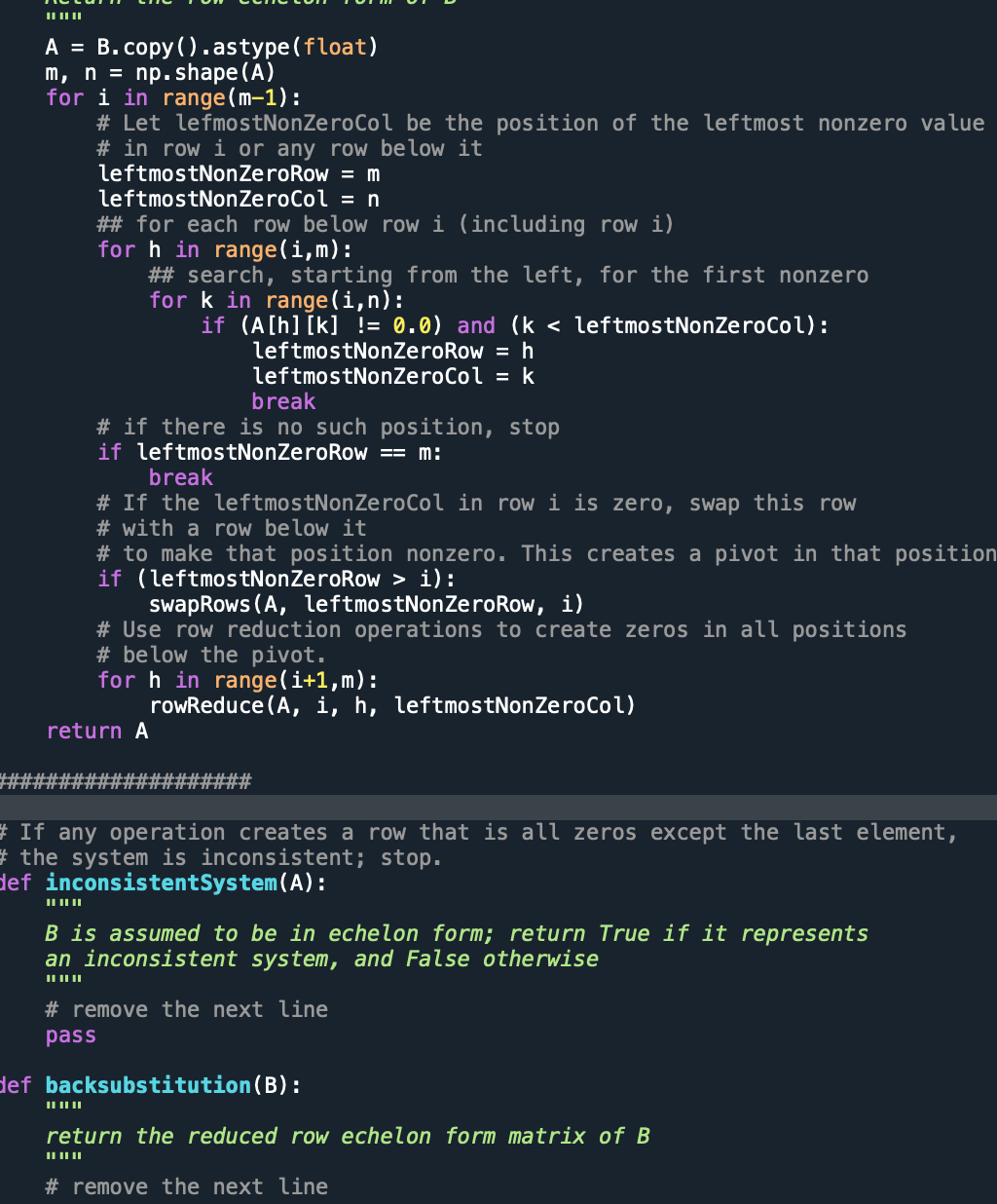
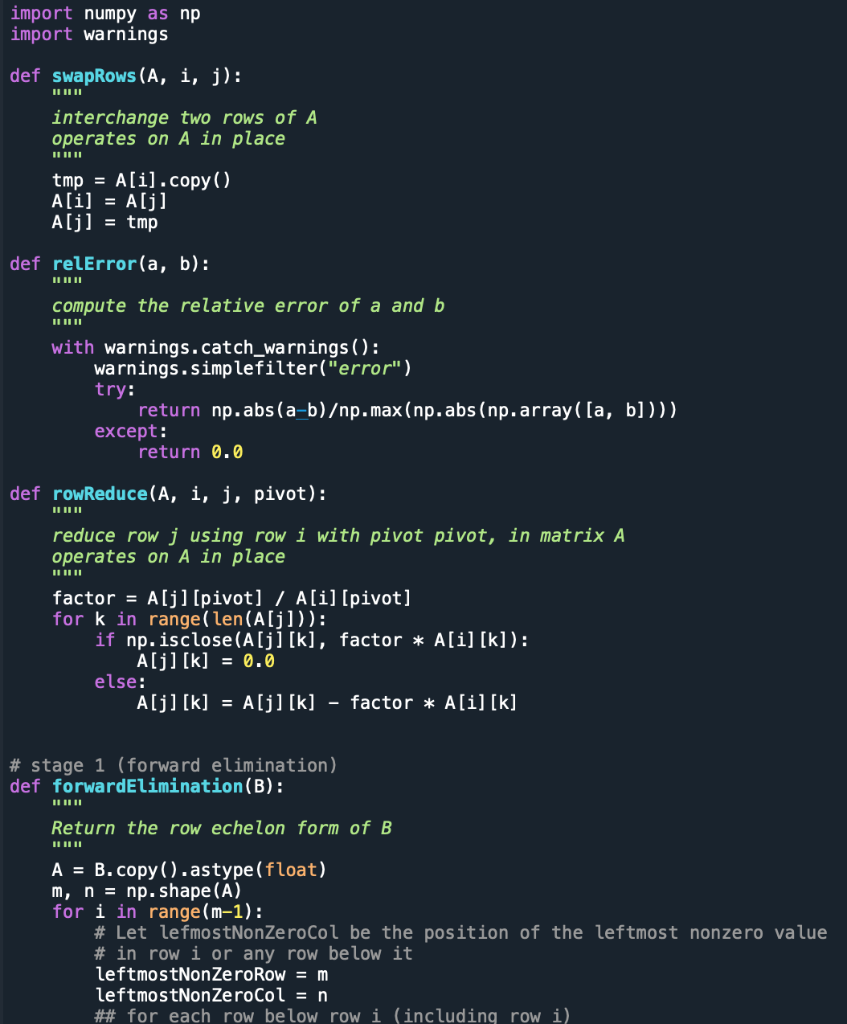
I have written the code for forward elimination. Your job is to provide the rest of the code and use the resulting set of functions to analyze some linear systems. (In case it helps, the code you have to write is (quite a bit) shorter than the code I have already supplied!) In hw2GECode.py I have provided the function: forwardElimination (B) which takes a matrix (numpy array) B and returns a new matrix that is the row echelon form of B. There are also helper functions in that file, for doing things like swapping rows of a matrix, doing row reduction, etc. You need two write two functions: inconsistent System (B) which takes a matrix B in echelon form, and returns True if it represents an inconsistent system, and False otherwise; and back substitution (B) which returns the reduced row echelon form matrix of B. Using these, you should be able to analyze a matrix representing a linear system as follows: AEchelon = forwardElimination (A) if (! inconsistent System (AEchelon)): AReducedEchelon = back substitution (AEchelon) 2 and then by inspecting AReducedEchelon you should be able to write down the solution set for the linear system. Coding Requirement. There is a coding requirement designed to help you learn to write efficient code. The general principle is that you should try to operate on whole data objects - vectors or matrices as a unit whenever possible. Therefore, for this specific assignment, you must use the function np.nonzero () within the code you write for both inconsistent System () and backsubstitution (). Read the documentation on np.nonzero () available at https:/umpy.org/doc/stable/reference/ generatedumpy.nonzero.html. Using that, you will see that if you have a row i of matrix A (denoted A[i] in python) then the positions of the nonzero entries in A[i] can be found using np.nonzero (A[i])[0]. Use this fact when writing your code for both inconsistent System () and backsubstitution(). This will simplify your code, make the code clearer, and make the code more efficient. Hints. First, make sure you understand the writeups "Notes on Python. and Linear Algebra in Python. Second, I encourage you to read carefully the code that is already provided before starting to write your own code. Most of what you need to do can be patterned after code that is already provided, as long as you understand what the provided code is doing! Spyder File Edit Search Source Run Debug Consoles Projects Tools View Help 4 Tue Feb 1 11:42 Spyder n I > ED /Users/manhtran/Desktop/CS132/ps2/hwk02-distrib t /Users/manhtran/Desktop/CS132/ps2/hwko2-distrib/tw2GECode py Source Console Object X temp.py Xhw2GECode.py BH Usage 29 48 41 42 43 44 45 46 47 48 49 58 51 52 53 54 55 Here you can get help af any abject by pressing Cmd-1 in front of it, either on the Editor or the Console. Help can also be shown automatically after writing a left parenthesis next to an object. You can activate this behavior in Preferences > Help New lo Spyder? Read our Lutorial Return the row echelon form of B A = B. copy().astypelfloat) m, n = np. shape(A) for i in range(n-1): # Let IcfrostNonZeracol be the position of the leftnost nonzero valuc # in row 1 or any row below it leftnostNonZeroRo En leftnostNonZerocal = n # for cach row below row i (including row i) for h in rangelin: o search, starting from the left, for the first nonzero for k in rangel1.n): if (A[h] [k] != 0.4) and {k 1): swapRows(AleftnostNonZeroRow, 1) # Use row reduction operations to create zeros in all positions # below the pivot. for h in range(1+1,m): rowReduce(A, i, h, leftnostNonZeroCal) return A Help Variable Explorer Plots Files X Console 1/A 57 58 59 68 61 62 63 64 65 66 67 68 69 78 71 72 73 74 75 76 77 78 79 89 81 82 B3 84 85 86 B7 ************* # If any operation creates a row that is all zeras except the last element, # the system is inconsistent; stop. def inconsistent5ysten (A): - A is assumed to be in echelon forw; return True if it represents an inconsistent system, and False otherwise remove the next line pass Python 3.9.5 (default, May 25 zez1, 07:41:55) Type "copyright", "credits" or "license" for more information. IPython 7.29.0 -- An cnhanced Interactive Python. This version of python seems to be incorrectly compiled (internal generated filenames are not absolute). This may make the debugger niss breakpoints. Related bug: http://bugs.python.org/issue1666897 >> runfilel/Users/manhtran/Desktop/CS132/ps2/hwk2-distrib/hw2GECode.py', wdir="/Usersanhtran/Desktop/CS132/ps2/twk02-distrib's 55 BU det backsubstitution(B): return the reduced rom echelon for matrix af & #renove the next line IPython Console History internal (Python 3.9.5) Line 72, Coli ASCII LF ) LSP Python: ready RY . E. tv X ILULUI A = B. copy().astype(float) m, n = np. shape (A) for i in range(m-1): # Let lefmostNonZeroCol be the position of the leftmost nonzero value # in row i or any row below it leftmostNonZeroRow = m leftmostNonZerocol = n ## for each row below row i (including row i) for h in range(i,m): ## search, starting from the left, for the first nonzero for k in range(i,n): if (A[h] [K] != 0.0) and (k i): swapRows (A, leftmostNonZeroRow, i) # Use row reduction operations to create zeros in all positions # below the pivot. for h in range(i+1,m) : rowReduce (A, i, h, leftmostNonZeroCol) return A ####### # If any operation creates a row that is all zeros except the last element, # the system is inconsistent; stop. def inconsistentSystem(A): II ILI B is assumed to be in echelon form; return True if it represents an inconsistent system, and False otherwise II ILUL # remove the next line pass def backsubstitution (B): II ILUL return the reduced row echelon form matrix of B II ILI # remove the next line import numpy as np import warnings def swapRows (A, i, j): interchange two rows of A operates on A in place tmp = A[i].copy ( ) A[i] = A[j] A[j] = tmp def relError(a, b): compute the relative error of a and b with warnings.catch_warnings(): warnings.simplefilter("error") try: return np.abs(a+b)p.max(np.abs(np.array([a, b]))) except: return 0.0 def rowReduce(A, i, j, pivot): reduce row j using row i with pivot pivot, in matrix A operates on A in place factor = A[j][pivot] / A[i][pivot] for k in range (len(A[j])): if np.isclose(A[j][k], factor * A[i] [k]): A[j][k] = 0.0 else: A[j][k] = A[j][k] - factor * A[i][k] # stage 1 (forward elimination) def forwardElimination(B): Return the row echelon form of B A = B.copy().astype(float) m, n = np. shape (A) for i in range (m-1): # Let lefmostNonZeroCol be the position of the leftmost nonzero value # in row i or any row below it leftmostNonZeroRow = m leftmostNonZerocol = n ## for each row below row i (including row i)