Please help with this question, thank you!

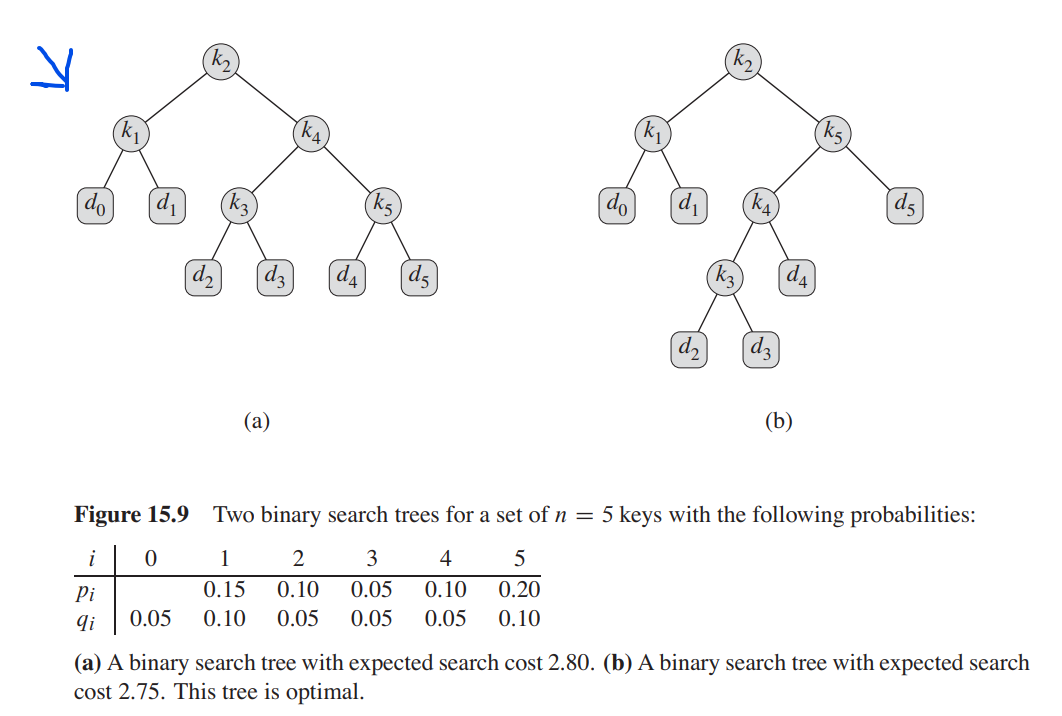
4. (20 points.) Its possible to print binary search trees (BSTs) using a functional notation. If K is the key at the root of a BST, L is the result of printing its left subtree, and R is the result of printing its right subtree, then we can print the BST as K(L, R). For example, the BST in figure 15.9 (a) on page 398 is printed like this.

k(k(d, d), k(k(d, d), k(d, d)))

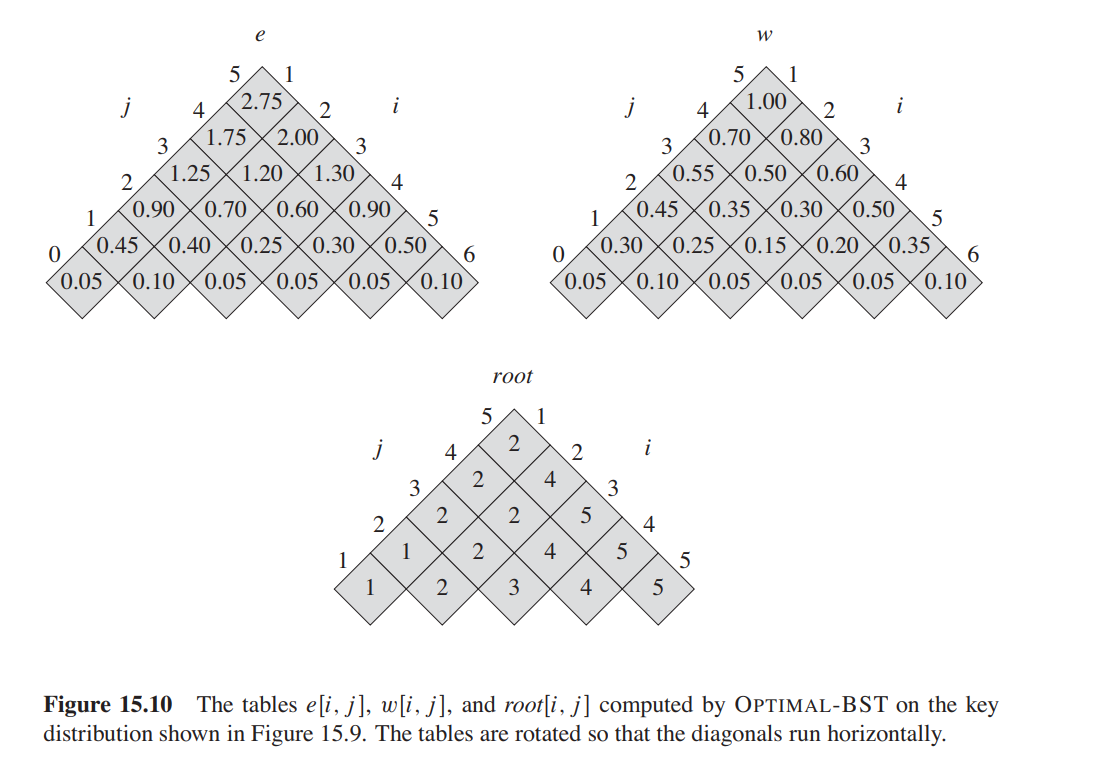
The procedure OPTIMAL-BST on page 402 returns a root matrix that represents an OBST. Write a procedure that takes such a root matrix as its argument, and prints it using the functional notation described above. For example, if your procedure is given the root matrix in figure 15.10 on page 403, then it must print this:

k(k(d, d), k(k(k(d, d), d), d))

Your procedure may call additional helper procedures. It need not print subscripts (like ), but can print ordinary digits (like 1) instead. For full credit, it must work correctly for any root matrix, not just the ones in the examples. You may write your procedure in pseudocode or in a programming language. It may be easier to use a programming language.

k, k V KA ks. do d ka ks do d k4 da (d, dz da (ds k3 (d4 d. dz (a) (b) Figure 15.9 Two binary search trees for a set of n = 5 keys with the following probabilities: i 0 1 2 3 4 5 Pi 0.15 0.10 0.05 0.10 0.20 li 0.05 0.10 0.05 0.05 0.05 0.10 (a) A binary search tree with expected search cost 2.80. (b) A binary search tree with expected search cost 2.75. This tree is optimal. e W j 3 5 1 4 2.75 2 i 3 1.75 2.00 3 2 1.25 1.20 1.30 4 1 0.90 0.70 0.60 0.90 5 0 0.45 0.40 0.25 0.30 0.50 6 0.05 0.10 0.05 0.05 0.05 0.10 5 1 4 1.00 2 i 0.70 0.80 3 2 0.55 0.50 0.60 4 1 0.45 0.35 0.30 0.50 5 0 0.30 0.25 0.15 0.20 0.35 6 0.05 0.10 0.05 0.05 0.05 0.10 root 5 1 2 2 i 2 4 3 3 2 2 2 5 4 1 2 4 1 5 5 1 2. 3 4 5 Figure 15.10 The tables e[i, j], w[i, j], and root[i, j] computed by OPTIMAL-BST on the key distribution shown in Figure 15.9. The tables are rotated so that the diagonals run horizontally. k, k V KA ks. do d ka ks do d k4 da (d, dz da (ds k3 (d4 d. dz (a) (b) Figure 15.9 Two binary search trees for a set of n = 5 keys with the following probabilities: i 0 1 2 3 4 5 Pi 0.15 0.10 0.05 0.10 0.20 li 0.05 0.10 0.05 0.05 0.05 0.10 (a) A binary search tree with expected search cost 2.80. (b) A binary search tree with expected search cost 2.75. This tree is optimal. e W j 3 5 1 4 2.75 2 i 3 1.75 2.00 3 2 1.25 1.20 1.30 4 1 0.90 0.70 0.60 0.90 5 0 0.45 0.40 0.25 0.30 0.50 6 0.05 0.10 0.05 0.05 0.05 0.10 5 1 4 1.00 2 i 0.70 0.80 3 2 0.55 0.50 0.60 4 1 0.45 0.35 0.30 0.50 5 0 0.30 0.25 0.15 0.20 0.35 6 0.05 0.10 0.05 0.05 0.05 0.10 root 5 1 2 2 i 2 4 3 3 2 2 2 5 4 1 2 4 1 5 5 1 2. 3 4 5 Figure 15.10 The tables e[i, j], w[i, j], and root[i, j] computed by OPTIMAL-BST on the key distribution shown in Figure 15.9. The tables are rotated so that the diagonals run horizontally