Please help with this question! Thank you!!

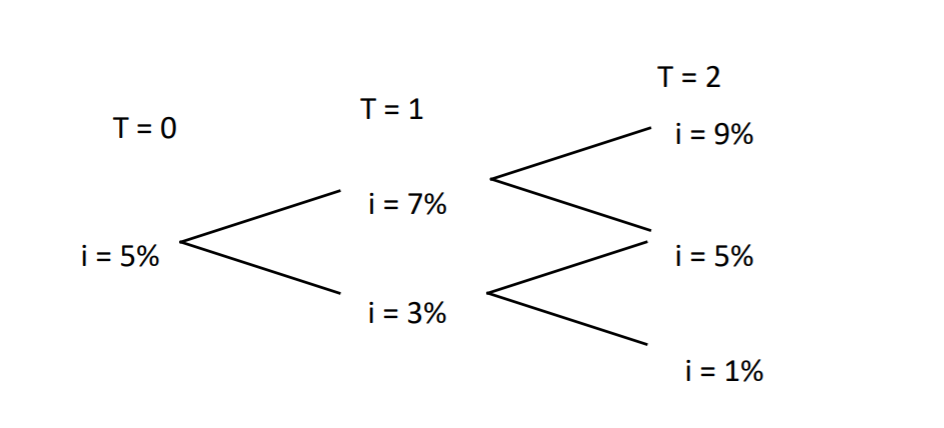
Consider the following evolution of interest rates, i. Price a 3-year zero-coupon bond (F=100) which is callable at 96 at T=1 and at 98 at T=2. You can (in approximation) view this bond as a portfolio of a long position in the zero coupon bond, a short position in a European call option with a strike price 96 and maturity T=1, and a short position in a European call option with a strike 98 and maturity T=2.

a) (12 points) What are the prices of an underlying non-callable zero coupon bond for each of the six nodes in the tree?

b) (8 points) Price a call option on the zero coupon bond in (a) with the strike price 96 and maturity T=1. i = 5% i = 7% i = 5% i = 1% i = 3% i = 9% T = 1 T = 0 T = 2 4

c) (15 points) Price a call option on the zero coupon bond in (a) with the strike price 98 and maturity T=2.

d) (5 points) What is the price of this bond? (Hint: The value of the option-embedded bond = Price of the zero coupon bond price of the two call options)

e) (5 points) Under what circumstances firms would want to issue callable bonds? Explain in fewer than three lines.

f) (5 points) Can callable bonds have negative convexity? Explain under what circumstances such negative convexity is possible (or impossible).

T = 2 T = 1 T = 0 i = 9% i = 7% i = 5% i = 5% i = 3% i = 1% T = 2 T = 1 T = 0 i = 9% i = 7% i = 5% i = 5% i = 3% i = 1%