please I need a new matlab code for this problem the one this person gave me does not give me the truss in the picture.

%Clear variables

clear all;

% *************************************************************************

% **** PRE-PROCESSING ****

% *************************************************************************

disp('PRE-PROCESSING...')

%----Set up model to be analyised----%

%Node positions

nodes = [0,325;

20,400;

500,400;

400,0;

825,0]*1e-3;

%Element connectivity matrix: C1 node 1, C2 node 2, R element no.

element_positions = [1,2;

2,3;

3,4;

1,4;

4,5;

3,5];

%Element Youngs modulus, can be same for all or matrix

element_modulus(1:size(element_positions,1),1) = 206*1e9;

%Forces acting on nodes: C1 Fx, C2 Fy, C3 M1, R node no.

nodal_force = [0,0,0;

0,-100,0;

0,-700,0;

0,0,0;

0,0,0];

%Boundary conditions on nodes: C1 Ux, C2 Uy, C3 M1, R node no.

%1 fixed, 0 free

nodal_boundary = [1,1,1;

0,0,0;

0,0,0;

0,0,0;

1,1,1];

%Element outer diameter, can be same for all or matrix with R element no.

element_diameters(1:size(element_positions,1),1) = 40*1e-3;

%Element inner diameter, can be same for all or matrix with R element no.

element_diameters(1:size(element_positions,1),2) = 36*1e-3;

%Type of element to be analised (rod, beam or frame)

% element_type = 'frame'

element_type = input('Element type (rod, beam, frame): ','s')

%----End of user inputs----%

%----Erroronous input catching----%

if size(nodes,1)

disp('Error: element position invalid given nodal cordinates')

elseif size(nodal_force,1) > size(nodes,1)

disp('Error: too many nodal forces')

elseif size(nodal_boundary,1) > size(nodes,1)

disp('Error: too many nodal boundaries')

elseif nodal_boundary ~= 1 | 0

disp('Error: invalid boundary condition')

end

%---------------------------------%

%Calculate element areas

element_area = pi()*(((element_diameters(:,1).^2)/4)-((element_diameters(:,2).^2)/4));

%Find diamention of the model

diamention = size(nodes,2);

%Global DOF of the model

globaldof = size(nodes,1)*size(nodes,2);

%Scale to increase visability of deformation on plot

scale=1000;

%Plot the object design

for i = 1:size(element_positions,1)

org = line(nodes(element_positions(i,1:2),1),nodes(element_positions(i,1:2),2));

set(org,'Marker','o','MarkerSize',10,'MarkerFaceColor','r')

end

% *************************************************************************

% **** SOLVER ****

% *************************************************************************

disp('SOLVING...')

%Find individual element stiffnesses in global cord

switch element_type

case 'rod'

%-----Create local stiffness matrix for each element-----%

% Create 3d matrix to store K for each element

Ke = zeros(4,4,size(element_positions,1));

for element = 1:size(element_positions,1)

%Get parameters

Ke_local = local_stiffness(nodes,element_positions,element_modulus,element_area,element_diameters,element_type,element);

angle = theta( nodes, element_positions, element);

T = trans_matrix(angle, element_type);

%Transform the element local stiffness matrix to global

Ke(:,:,element) = T' * Ke_local * T;

end

%-----Settings for globalising-----%

%Prepare the global stiffness matrix

K = zeros(globaldof,globaldof);

%Select node addition

node_depth = [1 2];

%Set node multiplier

n_multi = 2;

%Set flag not to skip moment in displacement scattering since not

%there

moment_skip = 0;

%Remove moment forces and boundary cond if present in matrices

nodal_force = [nodal_force(:,1),nodal_force(:,2)];

nodal_boundary = [nodal_boundary(:,1),nodal_boundary(:,2)];

case 'beam'

% Create 3d matrix to store K for each element

Ke = zeros(6,6,size(element_positions,1));

for element = 1:size(element_positions,1)

%Get parameters

Ke_local = local_stiffness(nodes,element_positions,element_modulus,element_area,element_diameters,element_type,element);

angle = theta( nodes, element_positions, element);

T = trans_matrix(angle, element_type);

%Transform the element local stiffness matrix to global

Ke(:,:,element) = T' * Ke_local * T;

end

%-----Settings for globalising-----%

%Prepare the global stiffness matrix

K = zeros(3*size(nodes,1),3*size(nodes,1));

%Set node depth

node_depth = [1 2 3];

%Set node multiplier

n_multi = 3;

%Set flag to skip moment in displacement scattering

moment_skip = 1;

case 'frame'

% Create 3d matrix to store K for each element

Ke = zeros(6,6,size(element_positions,1));

for element = 1:size(element_positions,1)

%Get parameters

Ke_local = local_stiffness(nodes,element_positions,element_modulus,element_area,element_diameters,element_type,element);

angle = theta( nodes, element_positions, element);

T = trans_matrix(angle, element_type);

%Transform the element local stiffness matrix to global

Ke(:,:,element) = T' * Ke_local * T;

end

%-----Settings for globalising-----%

%Prepare the global stiffness matrix

K = zeros(3*size(nodes,1),3*size(nodes,1));

%Using diamention of object, select node addition

node_depth = [1 2 3];

%Set node multiplier

n_multi = 3;

%Set flag to skip moment in displacement scattering

moment_skip = 1;

end

%----------------------------------------%

%-----Create global stiffness matrix-----%

%----------------------------------------%

%Construct global stiffness matrix

for element = 1:size(element_positions,1)

%Loop through nodes

for local_node_number_r = 1:size(nodes,2)

%Which global node does this refer too?

global_node_number_r = element_positions(element,local_node_number_r);

%Where do the terms belong in global matrix?

local_index_r = n_multi*( local_node_number_r - 1 ) + node_depth;

global_index_r = n_multi*( global_node_number_r - 1 ) + node_depth;

%Loop each column within row

for local_node_number_c = 1:size(nodes,2)

%Which global node?

global_node_number_c = element_positions(element,local_node_number_c);

%Where do terms belong in global matrix?

local_index_c = n_multi*( local_node_number_c - 1 ) + node_depth;

global_index_c = n_multi*( global_node_number_c - 1 ) + node_depth;

%Add terms correct places in global stiffness matrix

K(global_index_r,global_index_c) = K(global_index_r, global_index_c) ...

+ Ke(local_index_r, local_index_c, element);

end

end

end

%----Convert force matrix to vector----%

%Create empty force vector

F(1:(size(nodes,1)*n_multi),1) = 0;

%Zero column increment

h = 1;

%Convert force matrix to vector

for node_r = 1:size(nodal_force,1)

%For each row get the column force

for node_c = 1:size(nodal_force,2)

%Put the force into the vector F

F(h) = nodal_force(node_r, node_c);

h = h+1;

end

end

%----Apply boundary conditions----%

%First boundarys must be convertered to vector

%Create empty boundary vector

BC(1:(size(nodes,1)*n_multi),1) = 0;

%Zero column increment

h = 1;

%Convert boundary matrix to vector

for node_r = 1:size(nodal_boundary,1)

%For each row get the column force

for node_c = 1:size(nodal_boundary,2)

%Put the force into the vector F

BC(h) = nodal_boundary(node_r, node_c);

h = h+1;

end

end

%Loop to zero forces at boundaries

for i = 1:size(BC,1)

%If statement to set lines and columns coresponding to constrained

%point to zero

if BC(i) == 10;

K(i,:) = 0;

K(:,i) = 0;

%Set diagonal term to 1

K(i,i) = 1;

%Zero force at boundary

F(i) = 0;

end

end

%----------------------------------------%

%--------Find nodal displacement---------%

%----------------------------------------%

%Calculate displacement matrix

u = K\F;

% *************************************************************************

% **** POST-PROCESSING ****

% *************************************************************************

disp('POST-PROCESSING...')

%Convert displacement to nodal matrix

nodal_displacement(size(nodes,1),size(nodes,2)) = zeros;

h=1;

for node_r = 1:size(nodes,1)

for node_c = 1:size(nodes,2)

nodal_displacement(node_r,node_c) = u(h);

h=h+1;

end

%Flag to skip moment displacement since not used for strain

h=h+moment_skip;

end

nodes_displaced = nodes+(scale*nodal_displacement(:,1:2));

% for i = 1:size(element_positions,1)

% dis = line(nodes_displaced(element_positions(i,1:2),1),nodes_displaced(element_positions(i,1:2),2));

% set(dis,'LineStyle','--','Color','g','Marker','o','MarkerSize',5,'MarkerFaceColor','g')

% end

%Get length and change in length vectors

L = length_ele( nodes, element_positions );

d_L = length_delta( nodes, element_positions, nodal_displacement(:,1:2));

%Create nodal_area scalor

nodal_area(1:(size(nodes,1)*2),1) = 0;

i = 1;

for node_r = 1:size(element_area,1)

for h = 1:2

nodal_area(i) = element_area(node_r);

i=i+1;

end

end

%Calculate and output stress and strain

nodal_displacement

strain = (d_L-L) ./ L

stress = element_modulus .* strain

forces = stress .* element_area

This code gives me this error

Undefined function or variable 'n_multi'.

Error in HW3_2 (line 183) local_index_r = n_multi*( local_node_number_r - 1 ) + node_depth;

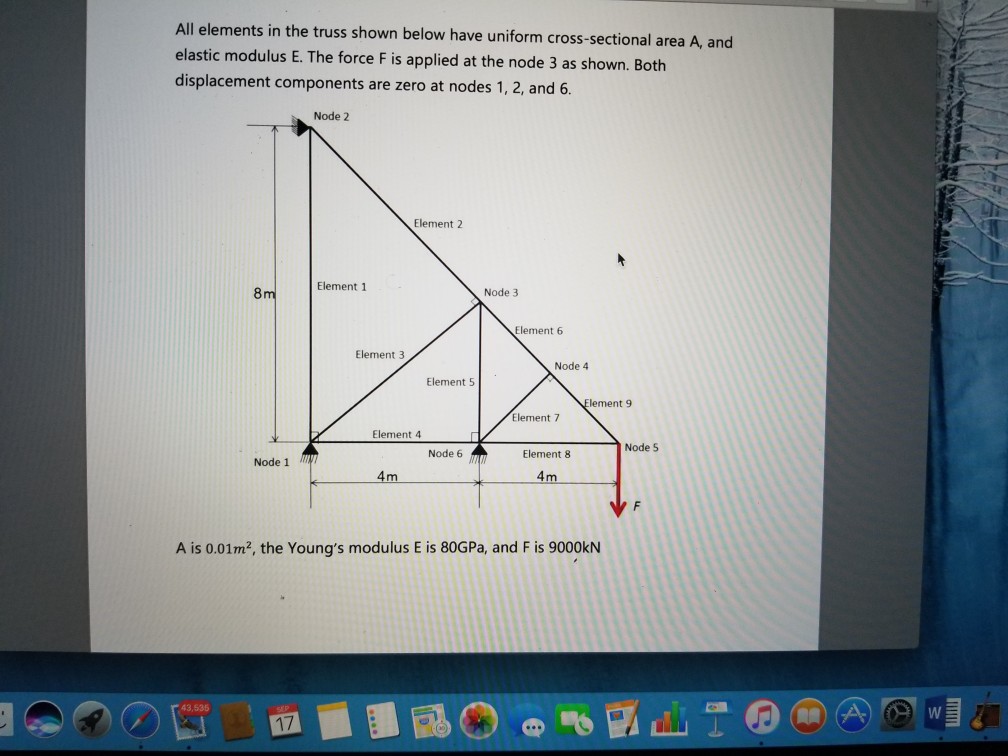
All elements in the truss shown below have uniform cross-sectional area A, and elastic modulus E. The force F is applied at the node 3 as shown. Both displacement components are zero at nodes 1, 2, and 6. Node 2 Element 2 Element 1 Node 3 8m Element 6 Element 3 Node 4 Element 5 lement 9 Element 7 Element 4 Node 5 Node 6 Element 8 Node 1 4m 4m A is 0.01m2, the Young's modulus E is 80GPa, and F is 9000kN 43,535 17