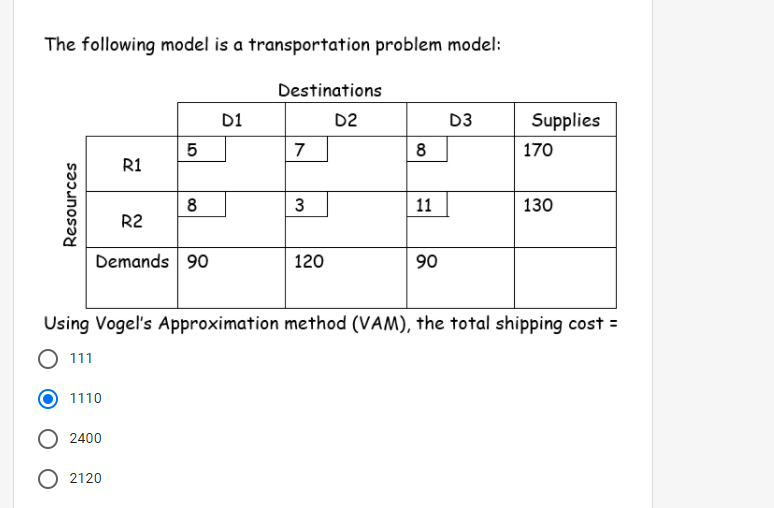
Question: please i need fast answer please The following model is a transportation problem model: D1 Destinations D2 7 D3 Supplies 170 01 8 R1 Resources



 please i need fast answer please
please i need fast answer please
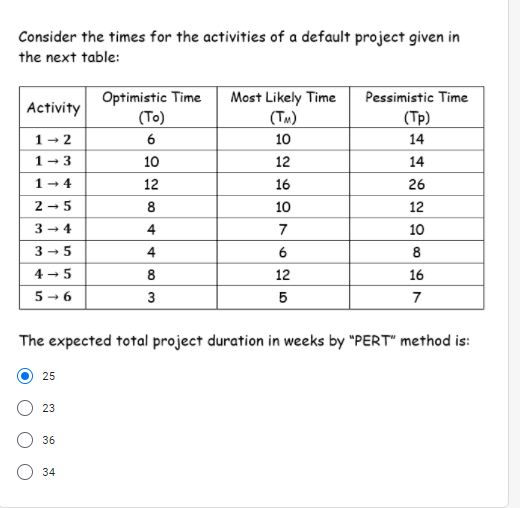
The following model is a transportation problem model: D1 Destinations D2 7 D3 Supplies 170 01 8 R1 Resources 8 3 11 130 R2 Demands 90 120 90 Using Vogel's Approximation method (VAM), the total shipping cost = 111 1110 2400 0 2120 For the LPP: Max. : Z = 8x1 + 6X2 Subject to: 2 x1 - x2 2 10 X1 + X2 S 30 where X1, x2 > 0 Using the Two-phase method, the new objective function in phase I is: Max.2 = 10x7 + 30x2 Max.r = R1 + R2 Option option Min.r = R2 + R2 Min.r = R1 Consider the times for the activities of a default project given in the next table: Most Likely Time Activity 1-2 1-3 14 2 - 5 34 35 4 - 5 Optimistic Time (To) 6 10 12 8 4 4 8 3 10 12 16 10 7 6 12 5 Pessimistic Time (Tp) 14 14 26 12 10 8 16 7 5-6 The expected total project duration in weeks by "PERT" method is: 25 23 36 34 The optimal solution of the LPP: Min. Z = 1.5x + 2.5y Subject to: x > 10 y = 20 where x,y > 0 By using the graphical method is: Min(z) = 0 at x = 0, y = 0 Min(z) = 15 at x = 10, y = 0 Option option Min(2) = 65 at x = 10, y = 20 Min(z) = 50 at x = 0, y = 20 Option Option. Consider the problem of assigning four operators to four machines. The assignment costs (in $/hour) are given below. Operator one cannot be assigned to machine three. Find the optimal assignment. Operator M1 015 027 03 9 04 7 Machine M2 M3 M4 5 2 4 2 3 3 5 19 2 6 7 01 for M3, 02 for M4,03 for M2, 04 for M1 01 for M4, 02 for M3,03 for M1, 04 for M2 01 for M4, 02 for M3,03 for M2, 04 for M1 01 for M1, 02 for M4,03 for M3,04 for M2 Consider the problem of assigning four operators to four machines. The assignment costs (in $/hour) are given below. Operator one cannot be assigned to machine three. Find the optimal assignment. Operator M1 015 027 03 9 04 7 Machine M2 M3 M4 5 2 4 2 3 3 5 19 2 6 7 01 for M3, 02 for M4,03 for M2, 04 for M1 01 for M4, 02 for M3,03 for M1, 04 for M2 01 for M4, 02 for M3,03 for M2, 04 for M1 01 for M1, 02 for M4,03 for M3,04 for M2





 please i need fast answer please
please i need fast answer please



