Question: Please I need help with this asap 3.4. Given A e RmxN, suppose that every m x m submatrix of A is invertible. For x

Please I need help with this asap

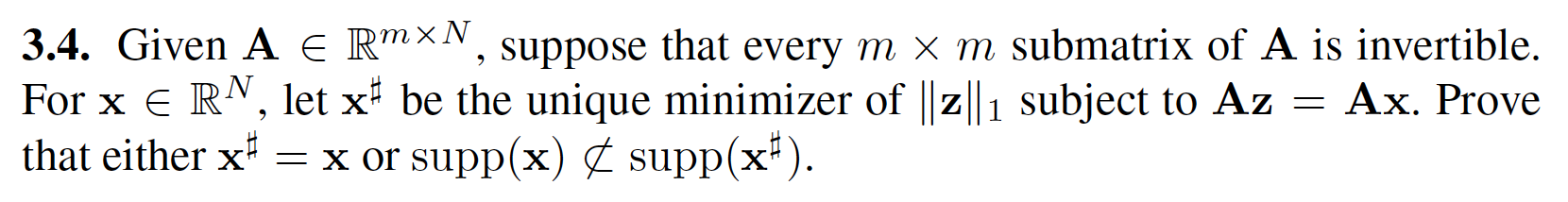
Please I need help with this asap 3.4. Given A e RmxN,

3.4. Given A e RmxN, suppose that every m x m submatrix of A is invertible. For x E RN, let x# be the unique minimizer of ||2||1 subject to Az = Ax. Prove that either x = x or supp(x) & supp(xF). 3.4. Given A e RmxN, suppose that every m x m submatrix of A is invertible. For x E RN, let x# be the unique minimizer of ||2||1 subject to Az = Ax. Prove that either x = x or supp(x) & supp(xF)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

1 1. (6+4+4+6) Let P3 denote the vector space of all third degree or less polynomials. (a) Find two linearly independent vectors in P3 that interpolate the data points (1, 2), (2, 1) and (3, 2). (b)...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

1 2.3 Definition of a Discrete Probability Function Definition: Let S be a discrete sample space from some experiment. A function P, defined on all events in S, is said to be a probability function...

Set Student Name: 1. Answer true or false for each part, and if false, explain your answer. a. The point estimate for the population mean, , of an x distribution is x-bar, computed from a random...

Explain why, on a busy system, key press echoes might be delayed when a high-priority user interacts with a low-priority application. Propose a solution, describing how each of the above system calls...

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

You are working for a firm that makes a special type of fertilizer that is sold in bags. They sell millions of these bags a year. Because of the accounting system, they claim that their fixed costs...

Gruneisen constant (a) Show that the free energy of a phonon mode of frequency w is k B T in [2sinh (hw/2k B T)]. It is necessary to retain the zero-point energy hw to obtain this result. (b) If is...

house. If che lnveats ecestatively and has a retam of 1 0 W per year, how much does she need to Invest ench month to hove thls amount in 5 year? No retrement ewhete when he tume c 3 . Acsume he wall...

3 25 pts Garden Life Enterprise plans to introduce various aged trees to their product range in 2022. They have provided the following information relating to its planned activities. Cherry Magnolia...