Please i provided two different homework the second one is already solve. This is to help you understanding how the first one should be done.

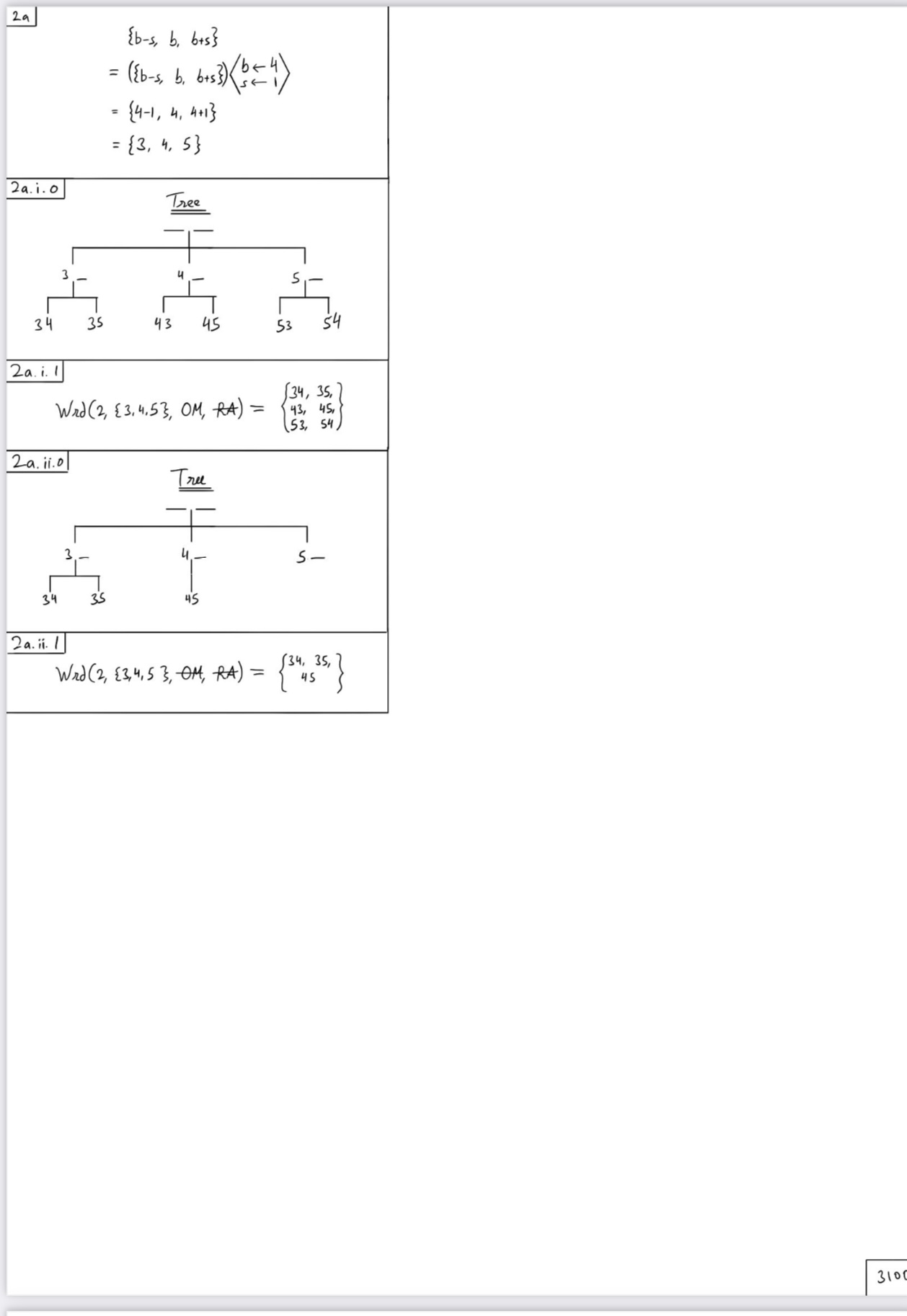
Instructions: Use these instructions for the remainder of the exam. Your J-number JN := (K E 0. .9/ k E 1..8) = 00380397 Hence J1 = 0 1 2 = 0 1 3 = 3 J4 = 6 1 5 =0 16 =3 17=2 18=7 R Write the elements of every numerical set or multiset appearing in this exam in increasing order. D U := 0.9 = {0, 1, 2, 3, 4, 5, 6, 7, 8,9} D SJ = St 1 := JK ED.. 9 K E 1 . .8 1 - 10 , 2 , 3 , 7 , 8 v ( SJ ) = 5 D List ( 1 := ( (SD) * EO.9 / KE 1 .. ( V (S1) ) ) = 10 , 2 , 3 , 7 , 8 D lu ( ( Is ) n ) .1 = 1 A lake it hi b.com D MSJ := MItst ( J ) := ($1)minm me 1. (v(S/) d 2 of 2 . 0 ction to leso Acad 27M subs - 10 :3 , 2 : 1 , 3 :2 , 7 :1, 8:1 6 news 6 year oduction to s discussed: at is Theory You may discuss with anyone 302D V(MSJ) = [mel. (v(s/) nm = 8 D S := mxm {k E 1..8Uk = 0} = 5 D b mnmUk E 0..9|odd(Jk)} = 3 D Define Y : = Yes N : = No Pf : = Proof W : = Witness D Z = XA Evn(x) x is even. D Z = XA Odd(x) x is odd. D NB XA Prm(x) x is prime. R Note that in a set an element may occur exactly once. Therefore, there may not be any repeated elements in any set in the above. So, if you do not have the correct sets, all your answers will be wrong. R If answers to different instances of some question on the exam contradict each other you will get a score of zero for every instance. R You will lose points for making any extraneous mark on the exam. R You may only submit complete answers to questions marked explicitly on the exam. You will lose points for unfinished work. R Separate pieces of work for any part of any problem recorded on a blank page intended for the purpose must be indexed by the index of the problem and also by numbers starting at 0 that record the order in which the pieces were completed; such parts must be separated from each other by straight lines parallel to the edges of the paper drawn with a ruler. You will lose points for otherwise. R Any sloppiness, untidiness, and any departure from proper format (as indicated in class) will lead to a score of 0. You may discuss with anyone 3036 (la) Compute, Vn E N, VK E 0..n the following, and express the result as a polynomial in n. Show computations or substitutions into appropriate formulas on pages that follow, numbered as per instructions, and write the answers on this page. You must use your own numbers before computing. 2 (i) 2 (ii) ce (v ( Must (1)). ( s.(1))) .( v ( s.(.)). ( s.(,))) ) S 2 (iii) c/ P (v( muse ( +)). ( muse (,)) ) . (w ( s.(.)). ( s (.)) )6 (1b) 3 (ii) Provide complete reasoning by making a systematic, exhaustive list in the form of a table, to generate, list, and count the following, showing all work on pages that follow, numbered as per instructions, and writing only the answers on this page: The symbol + means does not divide. D F:= (x,y)E 51(1) X St(]) x+y compute: F compute: V (F ) = _ II \"R W compute: G compute: V (G) = _ ll axN \\I-v-I' You may discuss with anyone 306 5 (1c) We define: p := n I> 2n(n + 1) =: N > N Prove without using induction that: Vn E N (4| (p(n))). Fill in the blank: Vn E N p(n) := Begin your proof on this page and continue onto pages that follow, numbered as per instructions. You may discuss with anyone 308 6 (2a) Use a tree (which you should draw on pages that follow, numbered as per instructions) to generate, list, and count the elements of the set of all 3-letter words in the alphabet [5, b} such that My {1,} = 3 (i) order matters and repetition is allowed, and Wrd 3,{ ],0M,RA = v Wrd 3, { , }, 0M, RA = 3 (ii) order does not matter and repetition is allowed Wt , ml U 1 J v Wrd 3,{ K J You may discuss with anyone 310 },QM,RA 6 (2b) Using a suitable tree (that should be displayed on pages that follow, numbered as per instructions) to generate, count, and list the elements of the set S of distinct 4digit numbers that may be made by using the elements of St ( j ) as digits: 5 || A _.,_ such that: o 0 cannot be used in the first place a the same digit occupies the first and fourth place, a the third digit is strictly larger than the second digit, and o the sum of the digits is even. E The 4digit number 2352 since 2 occupies the first and fourth positions, and 5 is strictly larger than 3 and the sum of the digits is 12, an even number. The 4digit number 2342 does not qualify as the sum of the digits is 11, not an even number. The number 2532 does not qualify as 3 is not strictly larger than 5. The number 2345 does not qualify as two distinct numbers occupy the first and fourth place. You may discuss with anyone 312 5 (2c) Find a recursive definition for the function defined below, indicating the base case(s) and recursive step explicitly. p = n- 2n(n + 1) =: N- N Write your answers on this page in the areas provided. 1 (i) BC 4 (1) RcS You may discuss with anyone 3146 (3a) Fill in the blanks appropriately on this page and answer the following: S = b = b+s= 1 (i) Compute, using the binomial theorem: BnmlCfn xbys, ( x + y ) ( ) ) = Bnmicfn ( x ( )y( ), (x+ > ) ( ) ) = 1 (ii) Compute, using the binomial theorem: Bnmicfn xsyb, ( x + y ) ( ) ) = Bnmicfn ( x ( )y( ), (x + y ) ( ) ) = 1 (iii) Compute, using the multinomial theorem: Mltnmicfn xbys, ( x + y) ( ) ) = Mlenmicfn (x( )y( ), (x+>) ( ) ) = 1 (iv) Compute, using the multinomial theorem: MltnmlCfn xsyb, ( x + y) ( ) ) = Mlenmicfn (x ( by( ), (x +y) ( ) ) = 1 (v) The answers in (i), (ii), (iii) and (iv) are equal; record answer on this page and work on the facing page: Y N Pf W 1 (vi) The answer to (v) depend on the values of s and of b; record answer on this page and work on the facing page: Y N Pf W You may discuss with anyone 3166 (3b) Fill in the blank appropriately, and show your work on pages that follow, numbered as per instructions, to compute the value of, after filling in the upper entry in the multinomial coefficient: Z (0 (p) q) p+q=4 You may discuss with anyone 317 5 (3c) Prove by induction that: Vn E N (4| (p(n))) using your recursive your recursive denition from (2c) for the function defined below: ,0: nI>2n(n+1)=:N>N Begin your work on this page and continue onto pages that follow, numbered as per instructions, as needed. 0 (i) B 0 (ii) H You may discuss with anyone 319 JN := (K E 0. .9| k E 1..8) = 4013 0 04 4 Hence J1=4 12=0 13=1 14=3 15=0 16=0 17=4 18=4 R Write the elements of every numerical set or multiset appearing in this exam in increasing order. D u := 0..9 = {0, 1, 2, 3, 4, 5, 6, 7, 8,9 } D SJ := St 1:= KEO.9 KE 18 - 1 0, 1, 3 , 4 v (SJ ) = 4 D List 1 := ((S/)k EO..9/K E 1.. (v(S/))) = ( 0, 1 3, 4 ) D ((IS)1) .13 1A D MSJ := Mitst ( J) :- CSDm: mm|mc 1.. (v(sp) = 0:3 , 1:1, 3:1, 4:3 D V(MSJ) EmEL(V(SD)) nm = 8 D S mnmke1.8 UkUk # 0} = You may discuss with anyone 302U er || mxmkE1__8{]k|k E 1. .8} = ['l D Define Y : = Yes N : = No Pf : = Proof W : = Witness D Vx E Z Evn(x) :4: x is even. D Vx E Z 0dd(x) : x is odd. D Vx E N Prm(x) :(=) x is prime. R Note that in a set an element may occur exactly once. Therefore, there may not be any repeated elements in any set in the above. So, if you do not have the correct sets, all your answers will be wrong. R If answers to different instances of some question on the exam contradict each other you will get a score of zero for every instance. R You will lose points for making any extraneous mark on the exam. R You may only submit complete answers to questions marked explicitly on the exam. You will lose points for unfinished work. R Separate pieces of work for any part of any problem recorded on a blank page intended for the purpose must be indexed by the index of the problem and also by numbers starting at 0 that record the order in which the pieces were completed; such parts must be separated from each other by straight lines parallel to the edges of the paper drawn with a ruler. You will lose points for otherwise. R Any sloppiness, untidiness, and any departure from proper format (as indicated in class) will lead to a score of 0. You may discuss with anyone 303 6 (la) Compute, Vn E N, VK E 0..n the following, and express the result as a polynomial in n. Show computations or substitutions into appropriate formulas exactly as shown in class on the facing page and write the answers on this page. 2 (1) c(c(v( s. (1)).0). ( ( Muse (,) ).0 ) ) = 2 (ii) = / 2 (iii) = ( 4 ! ) You may discuss with anyone 304la. i.o c (n , 0 ) = 1 ne vest J c ( v (St (J) ) , 0 ) = 1 la.i./ P ( n, 0 ) = 1 / new ( Must ( J) P (V ( Must ( J ) ) , 0 ) = 1 la. i.2 C C V ( St ( J ) 10 P ( ( MISS ( J ) ) 0 ) ) = C ( 1, 1 ) la. ii C (n , " ) = 1 no P(V (MHS+ (J ), v (st (J) c (P (Y ( MIS+ (J),7 (5+ (J) ) ),P( ( mast (J),7 ( s ( 5) )) = 1 la. ii.o P (n, n) = n! P (x ( MLEST ( J ) ), V ( MCS+ ( J ) ) ) = (V ( MUST (J) . ( 16 - V ( MUST ( J ) ) la. vi . I P ( nin) = n! P ( v(St (J ), " ( St (J) = (V(St(J)! (ne- w ( st (J ) la. ini. 2 c/ P (x ( MEESE ( J)), v ( MUSH ( J ) ) ), p ( x ( se (J)),( 5+ (J) ))) = C(1(v (Mlist (J > ! ) , ( ( v ( s t ( J ) ) ! ) ) = C ((81), (40) = ((4 !)) 30406 (1b) 3 (i) 3 (ii) Provide complete reasoning by making a systematic, exhaustive list in the form of a table, to generate, list, and count the following: D F: (x,y)E St(]) X St(]) x|y (0,0), (LO), (L!) (hi), (U1), (3.0), (53>, (a. o), (M) compute: F compute: 1,;(p) = i D 6:: (x,y)E St(]) K St(]) ylx (0,0), (0,0, (0,3), (om), } compute: G (u), (3 I), (3,3), (q, I). W1) II \"N compute: 12(0) = i You may discuss with anyone 306 \f6 (2a) Use a tree (which you should draw on the facing page) to generate, list, and count the elements of the set of all 2~letter words in the alphabet {b s, b, b + s} such that My {b-s,b,b+s}={ 3, ll, 5 } 3 (i) order matters and repetition is not allowed, and 3 H, as, Wrd 2,!1, Ll,5 Loam, = as, us, 53, S H II O\\ v Wrd 2,{ 3'q,51,om,a.4 3 (ii) order does not matter and repetition is not allowed L16 Wrd 213,143 1,944.34 v Wrd 213, H,51.9M.Ra4 = 3 You may discuss with anyone 310 \f