Please immediate assistance . I really need the help.

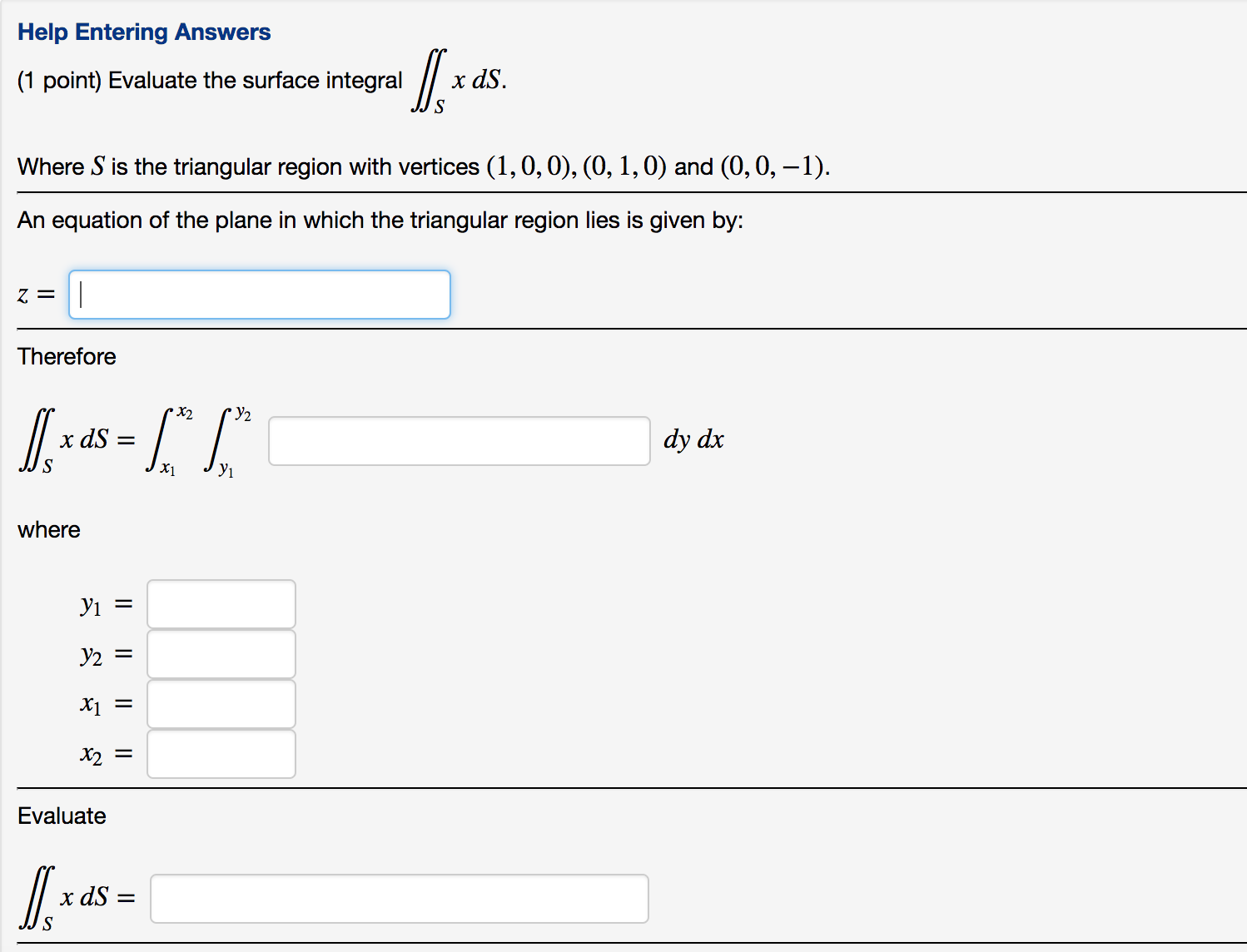
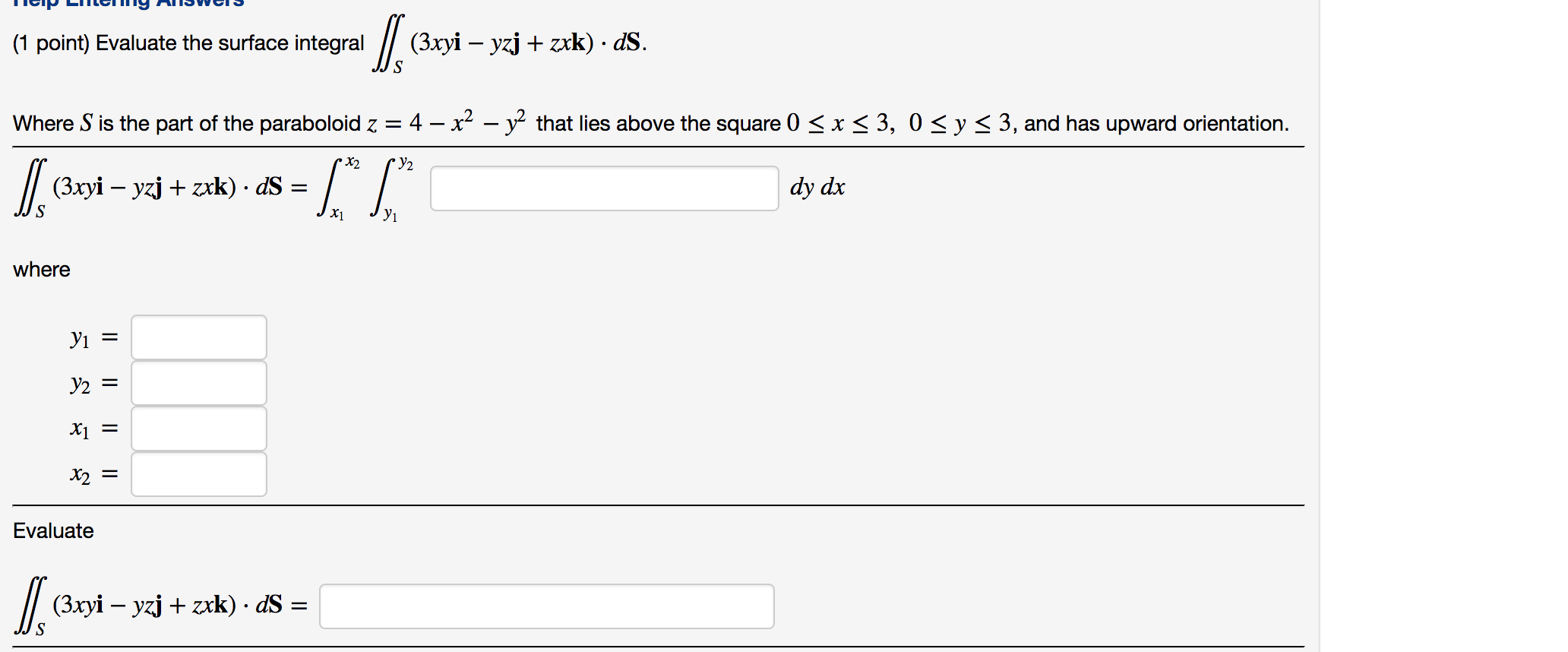
Help Entering Answers (1 point) Evaluate the surface integral [/16 d5. S Where S is the triangular region with vertices (1, 0, 0), (0, l, 0) and (0, 0, 1). An equation of the plane in which the triangular region lies is given by: F Therefore I2 3'2 j] x d5 = f / dy dx 5 J|f1 3'1 where 3'1 3'2 x1 x2 Evaluate flags: I IGIP IIIIGI "'5 HIIaIIGIB (1 point) Evaluate the surface integral (3xyi yzi + zxk) - ds. 3 Where S is the part of the paraboloid z = 4 x2 y2 that lies above the square 0 S x g 3, 0 g y g 3, and has upward orientation. x2 Y2 [/(3xyiyzj+zxk)'ds=/ / dydx S J61 Y1 where Y1 3'2 371 x2 Evaluate //(3xyiyzj+zxk)~ds= S . n... _...... ".3 . u... u... .- (1 point) Evaluate the surface integral (yj + zk) - dS . .9 Where S consists of the paraboloid y = x2 + 1,2,0 5 y S 4 and the disk 1:2 + 2,2 S 4,y = 4 , and has outward orientation. Consider splitting the surface into its parts S = S] U S2 where 51 is the paraboloid and S2 is the disk. Then we have SF-JS=-;lF-dsl+//SZF-ds2 31 can be parametrized by r1(s,t) = (scos(t), - ) Sz can be parametrized by r; (s,t) = (56050), - ) '2 52 '2 S2 //m-+zk>-ds=/ / :1/ / :W S :1 x1 t1 S1 (Evaluate S1 for the first blank and S2 for the second blank) Evaluate [gym-as: pi/2 ]+l4pi S (Evaluate $1 for the rst blank and S2 for the second blank) where