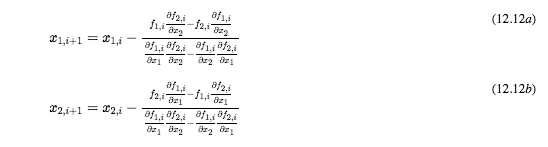
Please just write a single matlab code using all the necessary steps.

Solve the following simultaneous equations using the Newton-Raphson's method with guesses of * =1.5 and y=3.5: x + xy = 10 (1) y + 3xy2 = 57 (2) The stop condition is when both relative approximation errors are below 0.1%. Write one single program (not using the function) and output the solution in a table format with five columns Iteration No., *x', 'y', *.(x)', ',(y)' where ,(x) and (y) are the relative approximation errors of the variables x and y, respectively. In your program, you need to do the following three tasks. (a) Use the equations (12.12) to solve these two equations. (b) Use the equation (12.17) to solve these two equations with the Matlab matrix inverse function "inv" (c) Plot the two functions of (1) and (2) to graphically locate the solution and verify the solutions obtained from (a) and (b). You can use the interval of (0,4) for x to plot. Bf P/2. (12.12a) 21,1+1 = 21,1 8f1, 6f2, 0/1, 912, 2| 91, 0f2. (12.12b) 22,i+1 = 12, 8f1.: 9f2,; 8f1, 92, 1 12 {x;+1} = {x;} - [71-' (12.17) Solve the following simultaneous equations using the Newton-Raphson's method with guesses of * =1.5 and y=3.5: x + xy = 10 (1) y + 3xy2 = 57 (2) The stop condition is when both relative approximation errors are below 0.1%. Write one single program (not using the function) and output the solution in a table format with five columns Iteration No., *x', 'y', *.(x)', ',(y)' where ,(x) and (y) are the relative approximation errors of the variables x and y, respectively. In your program, you need to do the following three tasks. (a) Use the equations (12.12) to solve these two equations. (b) Use the equation (12.17) to solve these two equations with the Matlab matrix inverse function "inv" (c) Plot the two functions of (1) and (2) to graphically locate the solution and verify the solutions obtained from (a) and (b). You can use the interval of (0,4) for x to plot. Bf P/2. (12.12a) 21,1+1 = 21,1 8f1, 6f2, 0/1, 912, 2| 91, 0f2. (12.12b) 22,i+1 = 12, 8f1.: 9f2,; 8f1, 92, 1 12 {x;+1} = {x;} - [71-' (12.17)