please make it easy for me to understand properly thanks

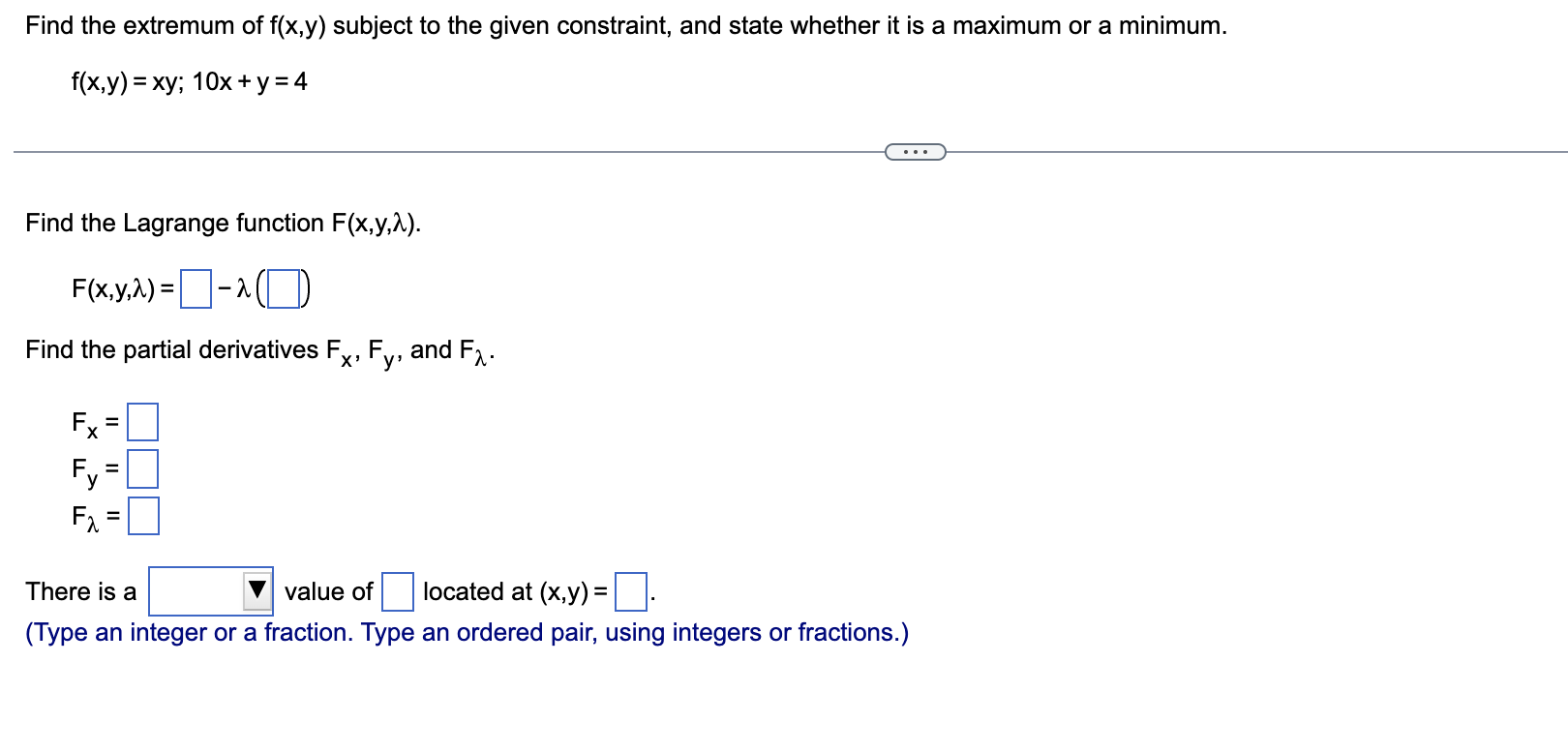
Of all points (x,y,z) that satisfy x + 5y + 2z =18, find the one that minimizes (x - 1)2 + (y - 1)2 + (z- 1)2. . . . The given function has a minimum at which satisfies x + 5y + 2z = 18. (Simplify your answer.)Find the extremum of f(x,y) subject to the given constraint, and state whether it is a maximum or a minimum. f(x.y)=ax2+y2w;x+y=2o There is a value of D located at (x, y) = Cl. (Simplify y( maximum minimum Find the extremum of f(x,y) subject to the given constraint, and state whether it is a maximum or a minimum. f(x,y) = xy; 10x + y = 4 . . . Find the Lagrange function F(x,y,a). F(x,y,2) = - Find the partial derivatives F , Fv, and Fx. Fx F, = There is a value of located at (x,y) = (Type an integer or a fraction. Type an ordered pair, using integers or fractions.)Find the extremum of f(x,y) subject to the given constraint, and state whether it is a maximum or a minimum. f(x,y) = 4x2 + 3y?; x+y= 14 . . . Find the Lagrange function F(x,y,2). F(x,y,A) = Find the partial derivatives FX, F, and Fx. F. F E There is a value of located at (x, y) = 7. (Type an integer or a fraction. Type an ordered pair, using integers or fractions.)Of all the numbers whose difference is 56, nd the two that have the minimum product. The two numbers whose difference is 56 and that have the minimum product are D. (Simplify your answer. Use a comma to separate answers as needed.)