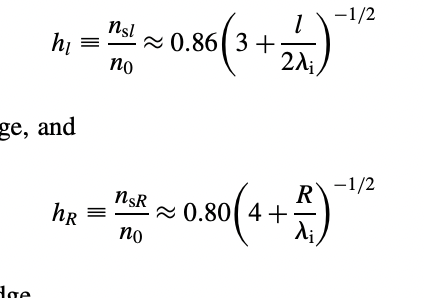
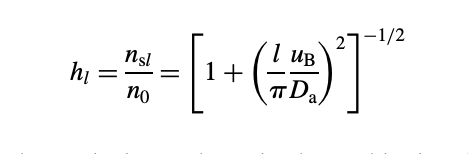
PLEASE NEW ANSWER, LAST ANSWER TO THIS QUESTION WAS NOT GOOD, HERE ARE EQUATIONS FOR EACH PROBLEM PART

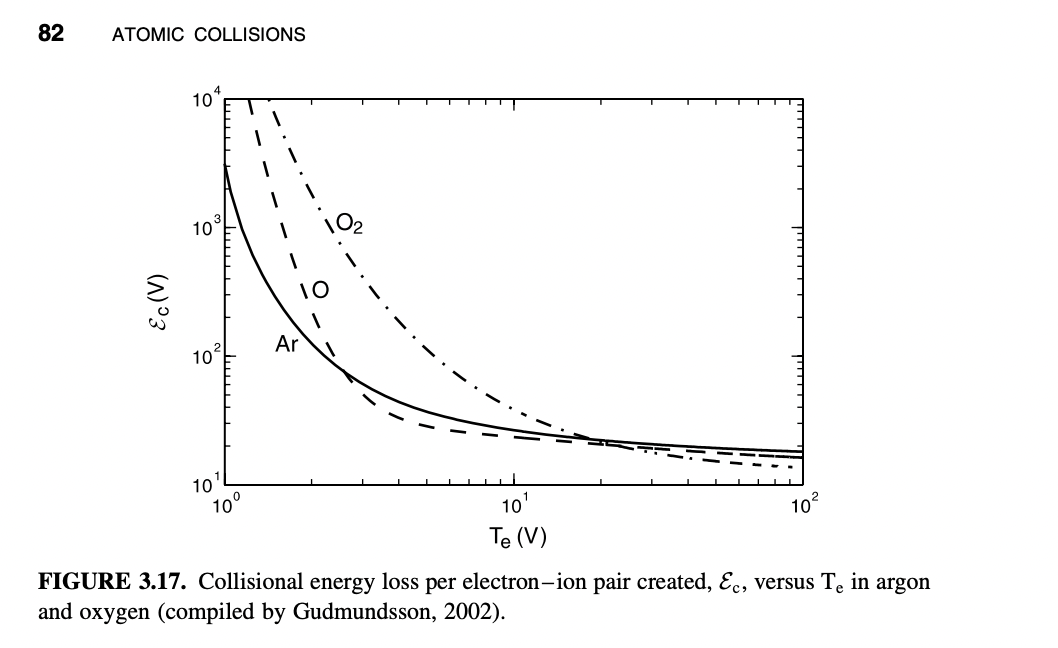
Consider the same cylindrical vacuum chamber you had in last week's homework, problem number 2: Ar gas in a 10cm radius chamber. Pick 1 Torr as the pressure, and say that the vertical length of the chamber is 60cm. From your last week's homework, you should already now know the electron temperature. a) Use figure 3.17 to find the energy needed to create an electron-ion pair, and use that value in the rest of the problem. b) Assume the power absorbed in this plasma is 1000W. Use the "Completely Uniform Density Mode" to find the density of the plasma. This assumes the hR and h1 factors are equal to 1 . c) Use the formulas in section 10.2 of L \& L to find the correct values of the "h" factors, and then find the density at the center of the discharge. d) Use the ambipolar diffusion "Non-Uniform Discharge Model" to find the density of the plasma (pp 336 to 337) at its center. e) Discuss the difference between parts b, c, and d. 82 ATOMIC COLLISIONS FIGURE 3.17. Collisional energy loss per electron-ion pair created, Ec, versus Te in argon and oxygen (compiled by Gudmundsson, 2002). hln0nsl0.86(3+2il)1/2 ge, and hRn0nsR0.80(4+iR)1/2 hl=n0nsl=[1+(lDauB)2]1/2 Equation (10.2.20) expresses the overall particle conservation in a nonuniform plasma slab, in analogy to (10.2.10), which expresses this same conservation for a finite cylinder of plasma with uniform bulk density except near the edges. Substituting (10.2.18) and (10.2.19) with x=l/2 into (10.2.20) and performing the integration, we obtain lDa=lKizng Since Da=MngKmieTe where Kmi(Ti) is the ion-neutral momentum transfer rate constant, and substituting uB=(eTe/M)1/2,(10.2.21) can be rewritten uB(Te)[KmiKiz(Te)]1/2=ngl Equation (10.2.23) is analogous to (10.2.12) in that it determines Te for a given ngl. Similarly, equating the total power absorbed by a unit area of the discharge, Sabs, to the total power lost, we have Sabs=2i(l/2)e(Ee+Ei)+2eEc0l/2Kizngne(x)dx Using (10.2.20) to eliminate the integral in (10.2.24). We find Sabs=2i(l/2)eET Substituting (10.2.19) with sinl/2=1 into (10.2.25), and solving for n0, we obtain n0=2DaeETSabsl which is analogous to (10.2.15). This procedure can be generalized to a finite cylinder nonuniform discharge with a constant Da, which can be solved, as done in Section 5.2. Using the solution found there, for example, with the approximations of zero densities at the plasma edge with a thin sheath, then the particle conservation equation is 2RiR(R,z)dz+4il(r,l/2)rdr=Kizngni(r,z)2rdrdz dxdi=Kizngne where ne=ni and i=Dadxdni to obtain the density ni and particle flux i. The results (5.2.22) and (5.2.24), repeated here, are ni(x)i(x)=n0cosx=Dan0sinx with Da the constant ambipolar diffusion coefficient. The simplest assumption made to obtain a solution is that ni0 at x=l/2 which gives =/l. This is reasonable because il [See discussion following (5.2.25)]. Integrating (10.2.16) from x=0 to x=l/2, we obtain i(l/2)=Kizng0//2ni(x)dx