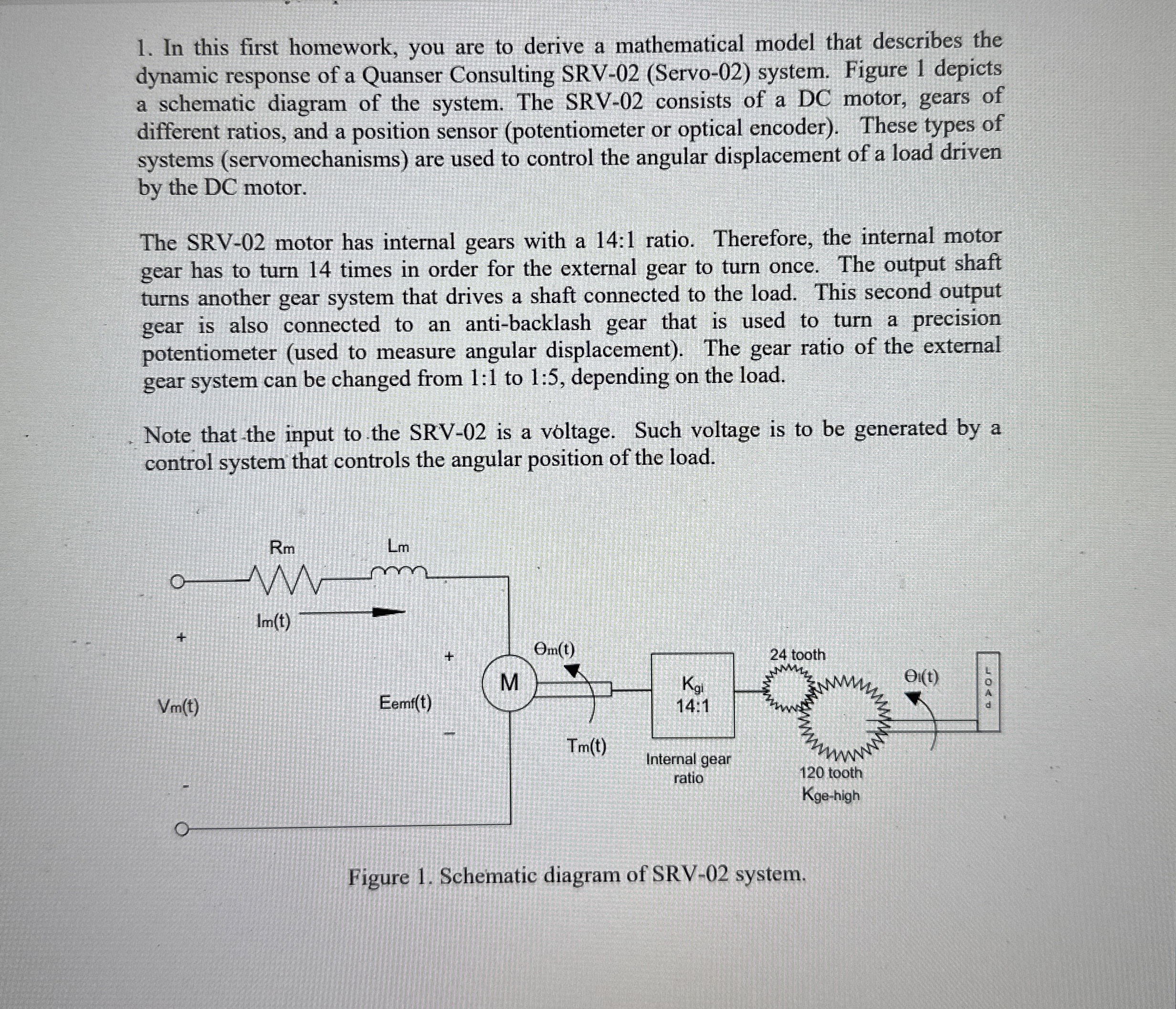
$($please note in the first page, motor internal gears with a $14$:$1$ ratio! not $1$:$14!)$ In this first homework, you are to derive a mathematical model that describes the dynamic response of a Quanser Consulting SRV$-02($Servo$-02)$ system. Figure $1$ depicts a schematic diagram of the system. The SRV$-02$ consists of a DC motor, gears of different ratios, and a position sensor $($potentiometer or optical encoder$).$ These types of systems $($servomechanisms$)$ are used to control the angular displacement of a load driven by the DC motor. Table $1.$ System's electrical and mechanical parameters.

$\backslash$table$[[$Symbol$,$Name,Value,Units$],[$K$\_($t$),$Motor Torque Constant,$0\mathrm{.}00767,$N$*$m$/$Amps$],[$K$\_($m$),$Back EMF Constant,$0\mathrm{.}00767,$V$/($rad$/$s$)],[$R$\_($m$),$Armature Resistance,$2\mathrm{.}6,\backslash$Omega $],[$K$\_($gi$),$Gearbox Ratio $($Internal$),14$:$1,$N$/$A$],[$K$\_($ge$-$high $),$External High Gear Ratio,$5$:$1,$N$/$A$],[$K$\_($ge$-$low $),$External Low Gear Ratio,$1$:$1,$N$/$A$],[$J$\_($m$),$Motor Inertia,$3\mathrm{.}87$e$-7,$kg$*$m$^(2)],[$J$\_($tach $),$Tachometer Inertia,$0\mathrm{.}7$e$-7,$kg$*$m$^(2)],[$Jeq$-$low,Equivalent Low Gear Inertia,$9\mathrm{.}3$e$-5,$kg$*$m$^(2)],[$J$\_($eq$-$high $),$Equivalent High Gear Inertia,$2\mathrm{.}0$ e$-3,$kg$*$m$^(2)],[$J$\_($arm$-$at$-$end $),$Arm$-$at$-$end inertia,$0\mathrm{.}001,$Kg$*$m$^(2)],[$J$\_($ge$)-120$ tooth,$120$ tooth gear inertia,$2\mathrm{.}27$ e$-5,$Kg$*$m$^(2)],[$Jarm$-$at$-$center,Arm$-$at$-$center inertia,$2\mathrm{.}75$ e$-4,$Kg$*$m$^(2)],[$L$\_($m$),$Armature inductance,$0\mathrm{.}18,$mH$],[$Jge$-72$ tooth,$72$ tooth gear inertia,$1\mathrm{.}4$ e$-6,$Kg$*$m$^(2)],[$Jge$-24$ tooth,$24$ tooth gear inertia,,Kg$*$m$^(2)],[$B$\_($eq$-$high $),\backslash$table$[[$Viscous Damping Coefficient$],[($High$)]],4\mathrm{.}0$e$^(-3),$N$*$m$/($rad$/$s$)],[$B$\_($eq$-$low $),\backslash$table$[[$Viscous Damping Coefficient$],[($Low$)]],1\mathrm{.}5$e$-3,$N$*$m$/($rad$/$s$)],[$K$\_($tach $),$Tachometer Sensitivity,$1\mathrm{.}5,$V$/1000$RPM$],[$Eff $\_($m $),$Motor Efficiency,$0\mathrm{.}69,$N$/$A$],[$Eff$,$Gearbox Efficiency,$0\mathrm{.}85,$N$/$A$]]$ The plant's transfer function is of the following form,

$\frac{{}_{r(s)}}{V_{m(s)}}=\frac{K_f}{s(s+p)}[ra\frac{d}{v}$olts$]$

where ${}_l$ is the angular displacement of the load, $V_m$ is the voltage applied to the motor, $K_f$

is the plant's constant and $p$ is the negative of the plant's pole.

a$)$ Write a set of differential and algebraic equations that are necessary and sufficient to

describe the dynamic response of the SRV$-02$ system. Use the parameters $($and their

respective symbols$)$ shown in Table $1.$

b$)$ Use the results obtained in part $a$ to determine the transfer function of the system.

c$)$ Explain the assumptions that were necessary to obtain the type of transfer function

specified in the problem,

$\frac{{}_{l(s)}}{V_{m(s)}}=\frac{K_f}{s(s+p)}[ra\frac{d}{v}$olts$]$

and determine the expressions for $K_f$ and $p$ in terms of the other system parameters.

The SRV$-02$ motor has internal gears with a $14$:$1$ ratio. Therefore, the internal motor gear has to turn $14$ times in order for the external gear to turn once. The output shaft turns another gear system that drives a shaft connected to the load. This second output gear is also connected to an anti$-$backlash gear that is used to turn a precision potentiometer $($used to measure angular displacement$).$ The gear ratio of the external gear system can be changed from $1$:$1$ to $1$:$5,$ depending on the load.

Note that the input to the SRV$-02$ is a voltage. Such voltage is to be generated by a control system that controls the angular position of the load.