*Please only answer if you know the answer I'm very strapped for time*

*To avoid confusion please highlight, circle, or box in the correct answer, that way I can differentiate between work and the correct answers*

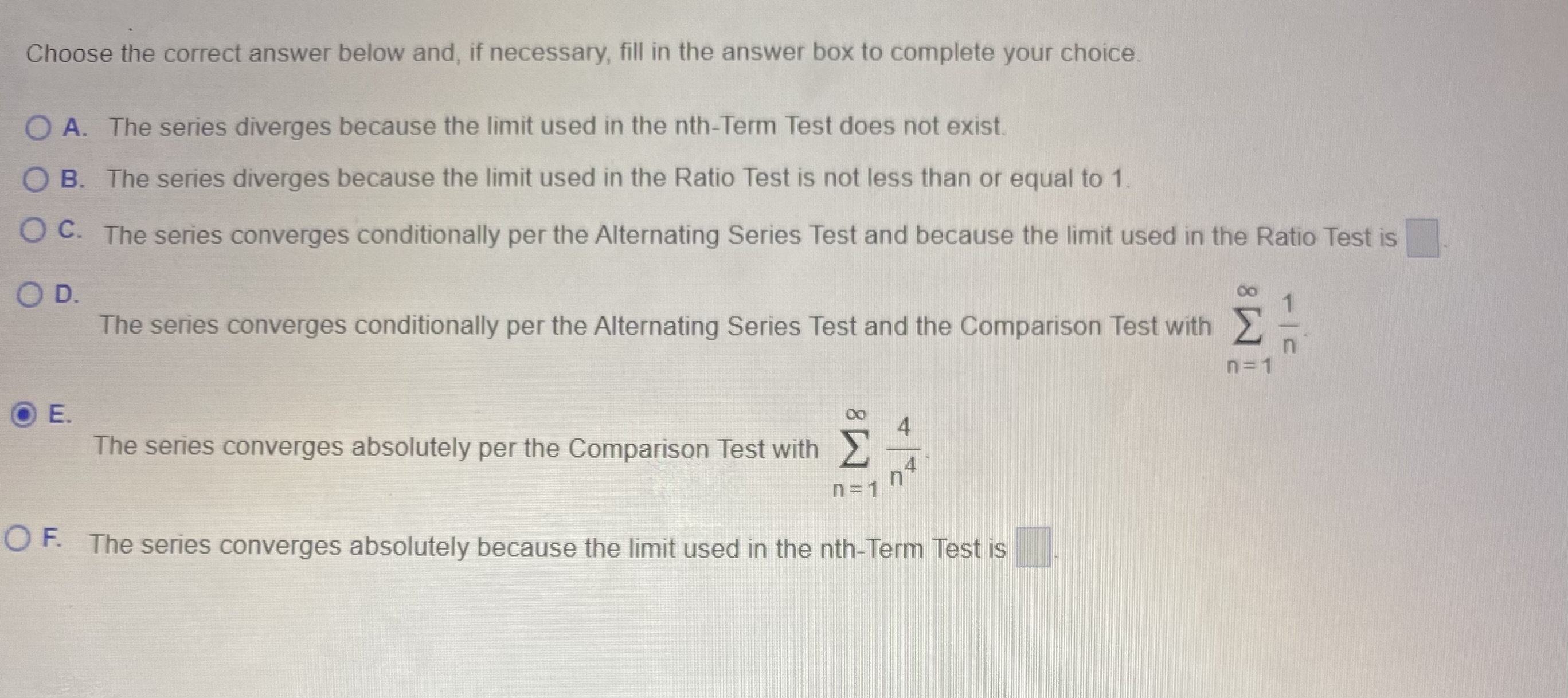
4 +13 Does the series converge absolutely, converge conditionally, or diverge? n = 1 1 4Choose the correct answer below and, if necessary, fill in the answer box to complete your choice O A. The series diverges because the limit used in the nth-Term Test does not exist. O B. The series diverges because the limit used in the Ratio Test is not less than or equal to 1. O C. The series converges conditionally per the Alternating Series Test and because the limit used in the Ratio Test is O D. The series converges conditionally per the Alternating Series Test and the Comparison Test with n n=1 OE. DO 4 The series converges absolutely per the Comparison Test with 4 n =1 O F. The series converges absolutely because the limit used in the nth-Term Test is