Please only answer the question a.

Please only answer the question a.

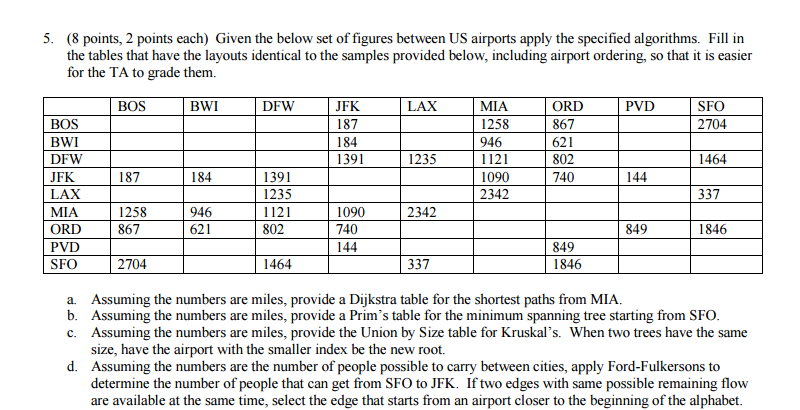
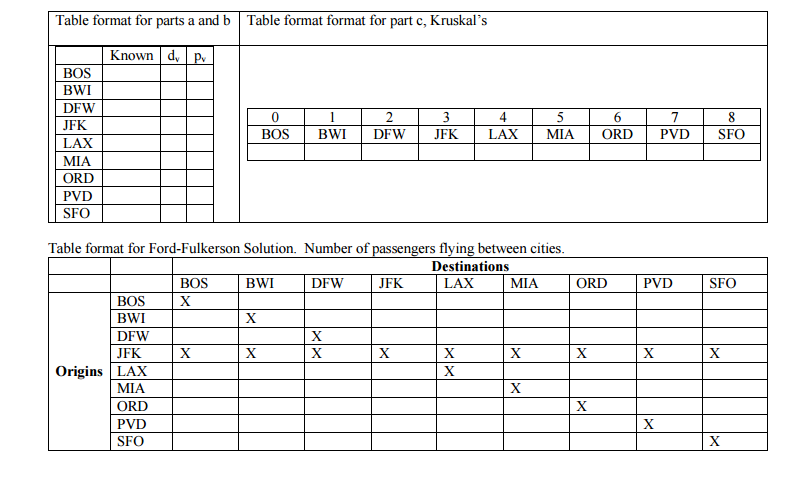
5. (8 points, 2 points each) Given the below set of figures between US airports apply the specified algorithms. Fill in the tables that have the layouts identical to the samples provided below, including airport ordering, so that it is easier for the TA to grade them. UFK 187 184 1391 MIA 258 946 1121 1090 2342 BOS DFW LAX ORD 867 621 802 740 BWI PVD SFO BOS BWI DFW JFK LAX MIA ORD PVD SFO 2704 1464 337 1846 1235 187 184 144 1391 1235 1121 802 1258 867 1090 740 144 2342 946 621 849 849 846 2704 1464 337 a. Assuming the numbers are miles, provide a Dijkstra table for the shortest paths from MIA. b. Assuming the numbers are miles, provide a Prim's table for the minimum spanning tree starting from SFO c. Assuming the numbers are miles, provide the Union by Size table for Kruskal's. When two trees have the same size, have the airport with the smaller index be the new root. Assuming the numbers are the number of people possible to carry between cities, apply Ford-Fulkersons to determine the number of people that can get from SFO to JFK. If two edges with same possible remaining flow are available at the same time, select the edge that starts from an airport closer to the beginning of the alphabet. d. 5. (8 points, 2 points each) Given the below set of figures between US airports apply the specified algorithms. Fill in the tables that have the layouts identical to the samples provided below, including airport ordering, so that it is easier for the TA to grade them. UFK 187 184 1391 MIA 258 946 1121 1090 2342 BOS DFW LAX ORD 867 621 802 740 BWI PVD SFO BOS BWI DFW JFK LAX MIA ORD PVD SFO 2704 1464 337 1846 1235 187 184 144 1391 1235 1121 802 1258 867 1090 740 144 2342 946 621 849 849 846 2704 1464 337 a. Assuming the numbers are miles, provide a Dijkstra table for the shortest paths from MIA. b. Assuming the numbers are miles, provide a Prim's table for the minimum spanning tree starting from SFO c. Assuming the numbers are miles, provide the Union by Size table for Kruskal's. When two trees have the same size, have the airport with the smaller index be the new root. Assuming the numbers are the number of people possible to carry between cities, apply Ford-Fulkersons to determine the number of people that can get from SFO to JFK. If two edges with same possible remaining flow are available at the same time, select the edge that starts from an airport closer to the beginning of the alphabet. d