PLEASE ONLY SOLVE PART 4.

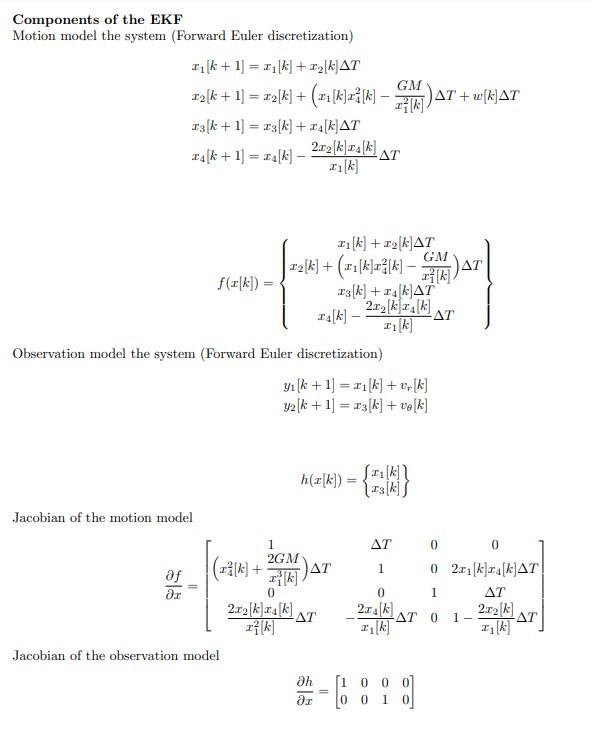
13.16 A planar model for a satellite orbiting around the earth can be modeled as r=r2r2GM+w=r2r where r is the distance of the satellite from the center of the earth, is the angular position of the satellite in its orbit, G=6.67421011m3/kg/s2 is the universal gravitational constant, M=5.981024kg is the mass of the earth, and w (0,106) is random noise due to space debris, atmospheric drag, outgassing, and so on. Components of the EKF Motion model the system (Forward Euler discretization) x1[k+1]=x1[k]+x2[k]Tx2[k+1]=x2[k]+(x1[k]x42[k]x12[k]GM)T+w[k]Tx3[k+1]=x3[k]+x4[k]Tx4[k+1]=x4[k]x1[k]2x2[k]x4[k]Tf(x[k])=x1[k]+x2[k]Tx2[k]+(x1[k]x42[k]x12[k]GM)Tx3[k]+x4[k]Tx4[k]x1[k]2x2[k]x4[k]T Observation model the system (Forward Euler discretization) y1[k+1]=x1[k]+vr[k]y2[k+1]=x3[k]+v[k] h(x[k])={x1[k]x3[k]} Jacobian of the motion model xf=1(x42[k]+x13[k]2GM)T0x12[k]2x2[k]x4[k]TT10x1[k]2x4[k]T001002x1[k]x4[k]TT1x1[k]2x2[k]T Jacobian of the observation model xh=[10000100] Problem 13.16 in textbook. However, skip steps relating to the linearized Kalman Filter (just do the EKF). That is, just do part (a), part (b), part (c), and part (e) without the comparing the performance. Note: The measurements and other details are described in part (d). Simulate the system dynamics and the EKF for 3 hours. 2. Use the same system and measurement models from problem 1, and obtain a solution using an Unscented Kalman Filter (UKF). Use the same system and measurement models from problem 1, and obtain a solution using a Particle Filter (PF). Be sure to justify your choice of number of particles. 4. Perform 20 3-hour runs with each method (from problems 1-3) and compare the RMS tracking error of radius as a function of time