please only work on Q3 & Q4

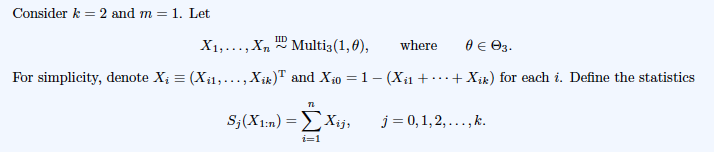
Consider k = 2 and m = 1. Let X1, . .., Xn - Multis (1, 0), where For simplicity, denote Xi = (Xi, ..., Xax) and Xin =1 -(Xu + .. . + Xik) for each i. Define the statistics S;(Xin) => Xijs j = 0, 1, 2, ..., k. i=11. (10%) Prove that the joint PMF of (X1, ..., Xn) is fo(T1in) = (1 -01 -02)" 61 S1(F1:n) 1 - 01 - 02 1 - 01 - 02 1(11, . . . . In (13). 2. Prove that T(Xin) = (S1(Xin), S(X1:n)) is a sufficient statistic (SS) for / by using (a) (15%) the definition of sufficiency; (b) (10%) Neyman-Fisher factorization theorem; and (c) (15%) the properties of exponential family. 3. (10%) Is T(X1:n) = (So(X1:), S1(X1:m)) also sufficient for e? Why? 4. & Let X1, .... X, ~ Multix(m, 0), where m, ke N are fixed, and ( e Ox+1. Find a SS for d by using (a)-(c) in part 2