Please provide explanations for 1 and 3

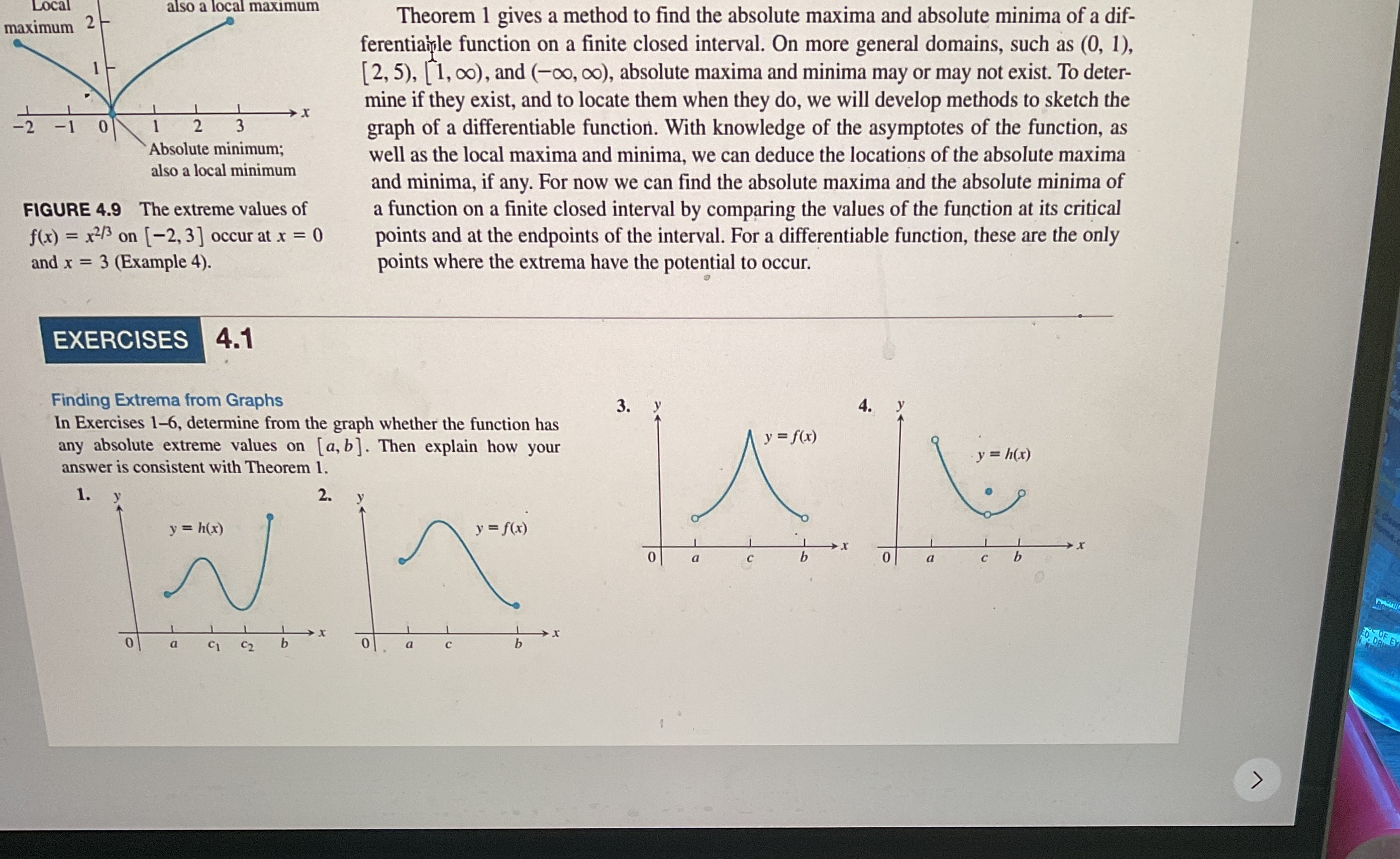
Local also a local maximum maximum 2 Theorem 1 gives a method to find the absolute maxima and absolute minima of a dif- ferentiample function on a finite closed interval. On more general domains, such as (0, 1), [2, 5), [1, 00), and (-oo, co), absolute maxima and minima may or may not exist. To deter- mine if they exist, and to locate them when they do, we will develop methods to sketch the 2 3 graph of a differentiable function. With knowledge of the asymptotes of the function, as Absolute minimum; also a local minimum well as the local maxima and minima, we can deduce the locations of the absolute maxima and minima, if any. For now we can find the absolute maxima and the absolute minima of FIGURE 4.9 The extreme values of a function on a finite closed interval by comparing the values of the function at its critical f(x) = x2/3 on [-2, 3 ] occur at x = 0 points and at the endpoints of the interval. For a differentiable function, these are the only and x = 3 (Example 4). points where the extrema have the potential to occur. EXERCISES 4.1 Finding Extrema from Graphs 3. 4. In Exercises 1-6, determine from the graph whether the function has any absolute extreme values on [a, b ]. Then explain how your y = f( x) y = h(x) answer is consistent with Theorem 1. 1. 2. y = h(x) y = f (x ) 0 0 a a ED OF C 2 b