Please provide explanations for 27, 31, 32

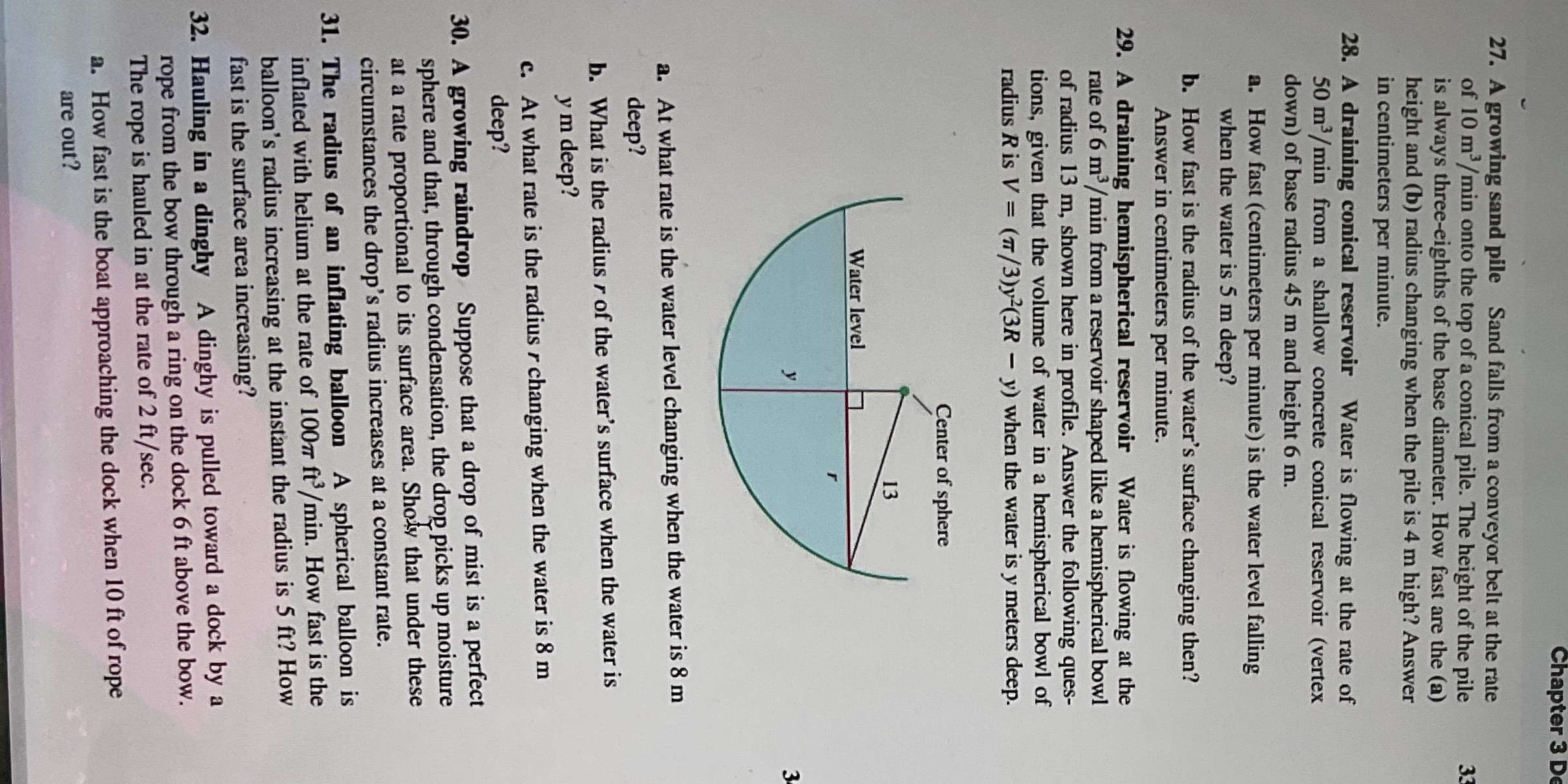
Chapter 3 D 27. A growing sand pile Sand falls from a conveyor belt at the rate of 10 m3/ min onto the top of a conical pile. The height of the pile is always three-eighths of the base diameter. How fast are the (a) height and (b) radius changing when the pile is 4 m high? Answer in centimeters per minute. 28. A draining conical reservoir Water is flowing at the rate of 50 m3/ min from a shallow concrete conical reservoir (vertex down) of base radius 45 m and height 6 m. a. How fast (centimeters per minute) is the water level falling when the water is 5 m deep? b. How fast is the radius of the water's surface changing then? Answer in centimeters per minute. 29. A draining hemispherical reservoir Water is flowing at the rate of 6 m/ min from a reservoir shaped like a hemispherical bowl of radius 13 m, shown here in profile. Answer the following ques- tions, given that the volume of water in a hemispherical bowl of radius R is V = (1/3)y2(3R - y) when the water is y meters deep. Center of sphere Water level a. At what rate is the water level changing when the water is 8 m deep? b. What is the radius r of the water's surface when the water is y m deep? c. At what rate is the radius r changing when the water is 8 m deep? 30. A growing raindrop Suppose that a drop of mist is a perfect sphere and that, through condensation, the drop picks up moisture at a rate proportional to its surface area. Sholy that under these circumstances the drop's radius increases at a constant rate. 31. The radius of an inflating balloon A spherical balloon is inflated with helium at the rate of 10077 ft3 / min. How fast is the balloon's radius increasing at the instant the radius is 5 ft? How fast is the surface area increasing? 32. Hauling in a dinghy A dinghy is pulled toward a dock by a rope from the bow through a ring on the dock 6 ft above the bow. The rope is hauled in at the rate of 2 ft/sec. a. How fast is the boat approaching the dock when 10 ft of rope are out