Please provide steps. Thx!

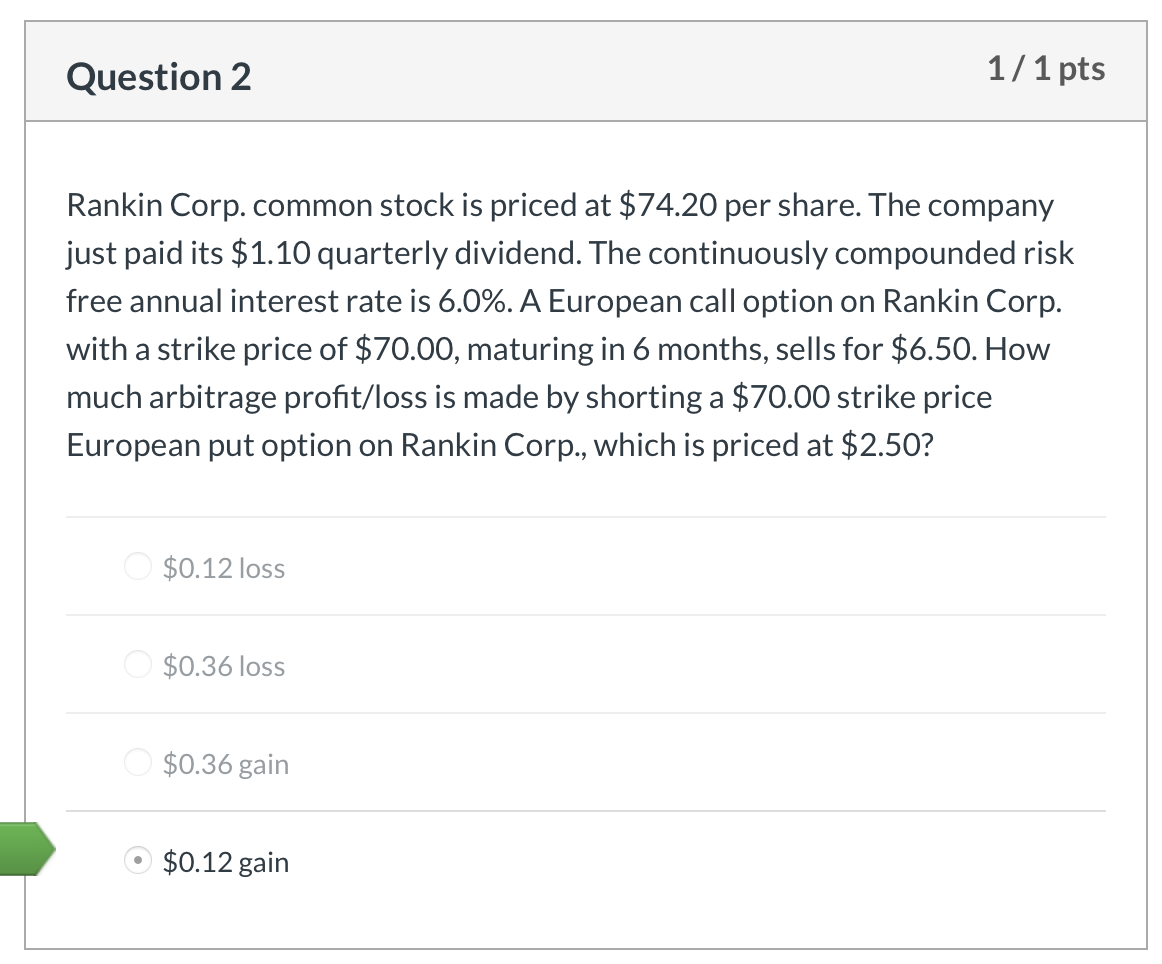
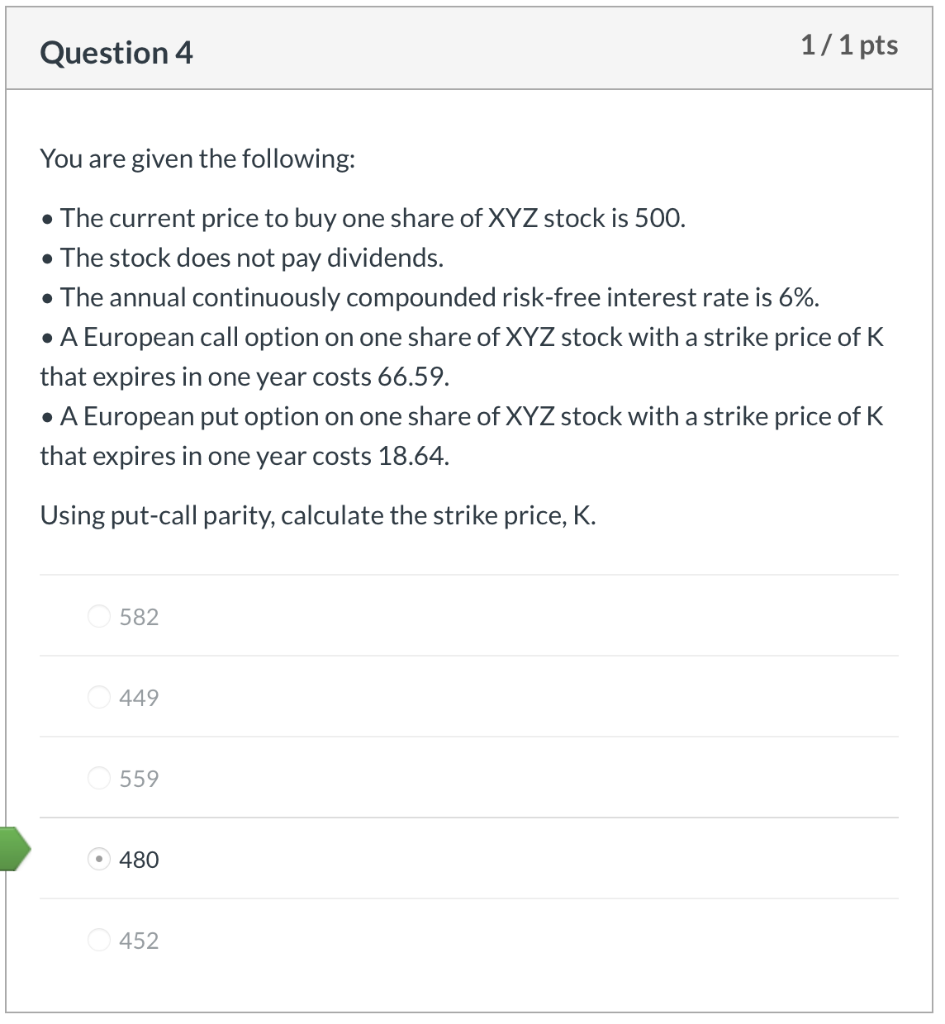
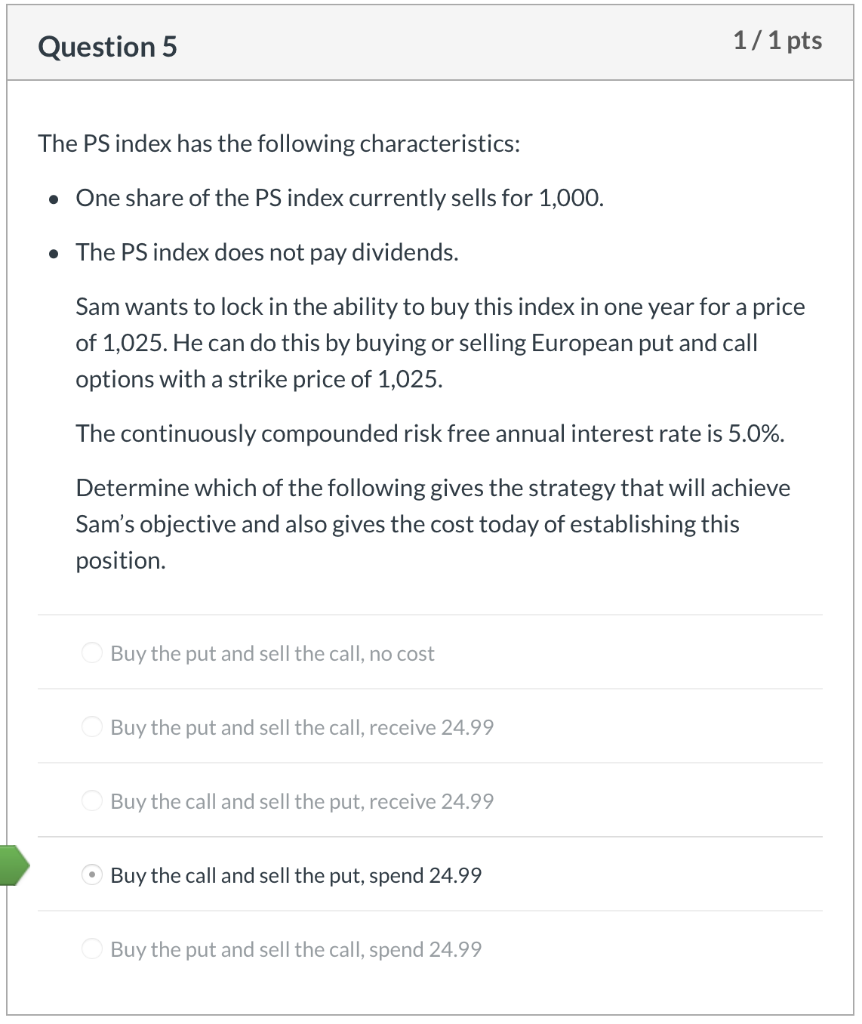
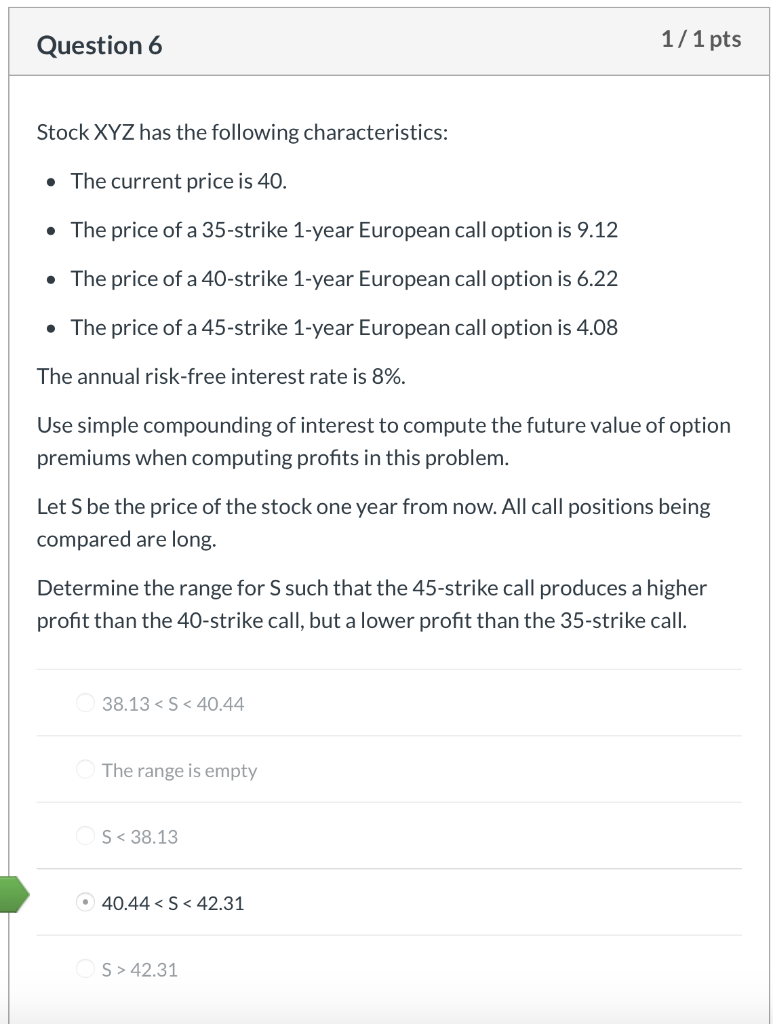
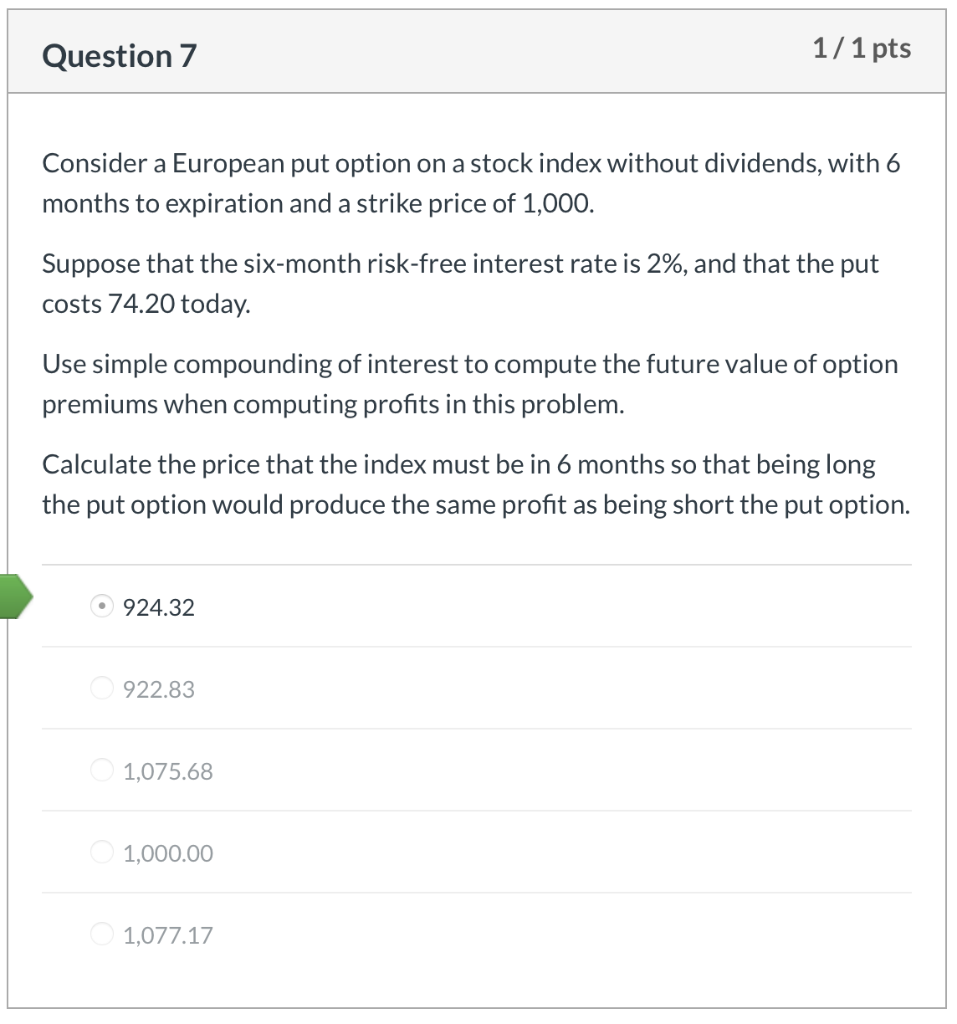
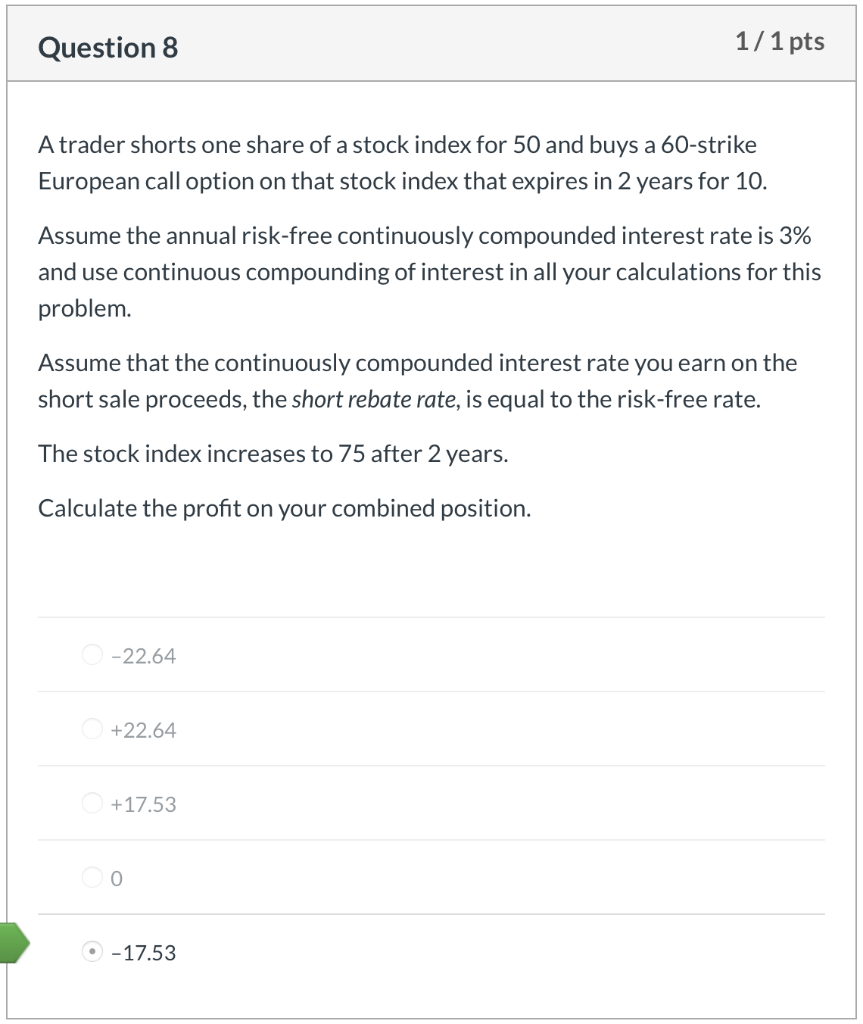
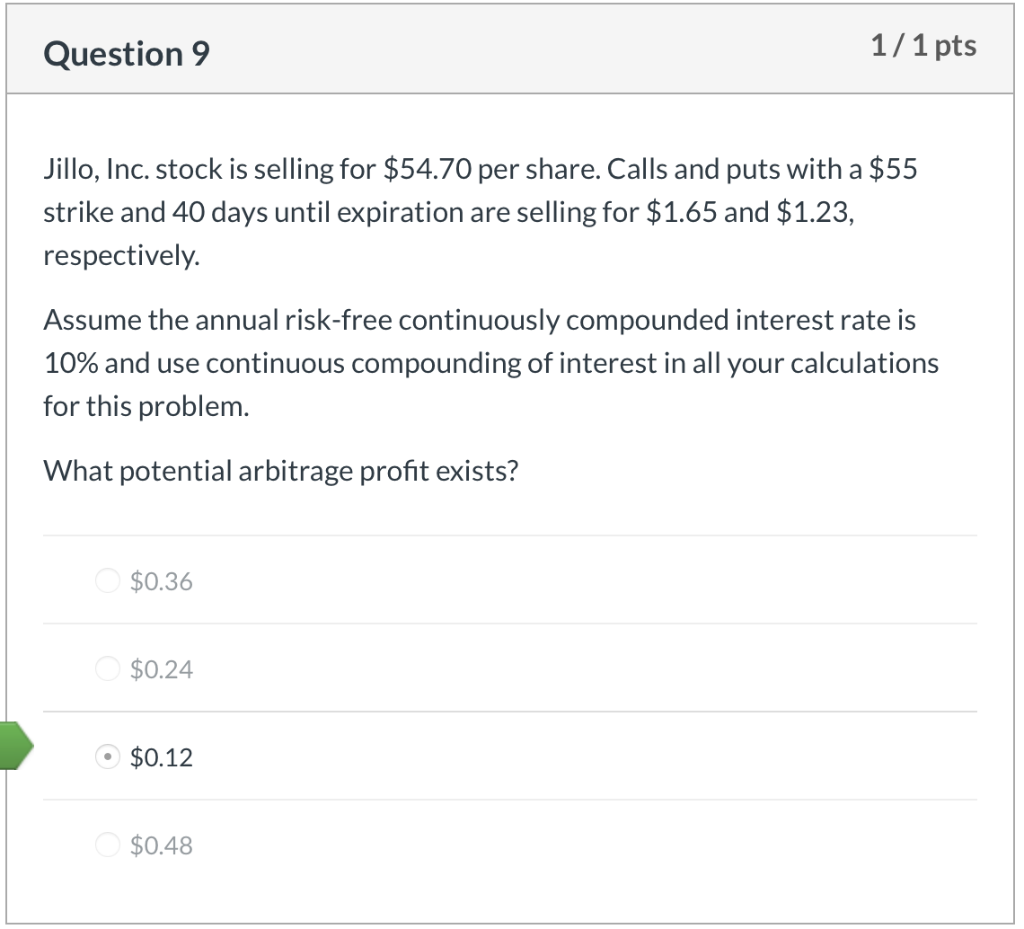
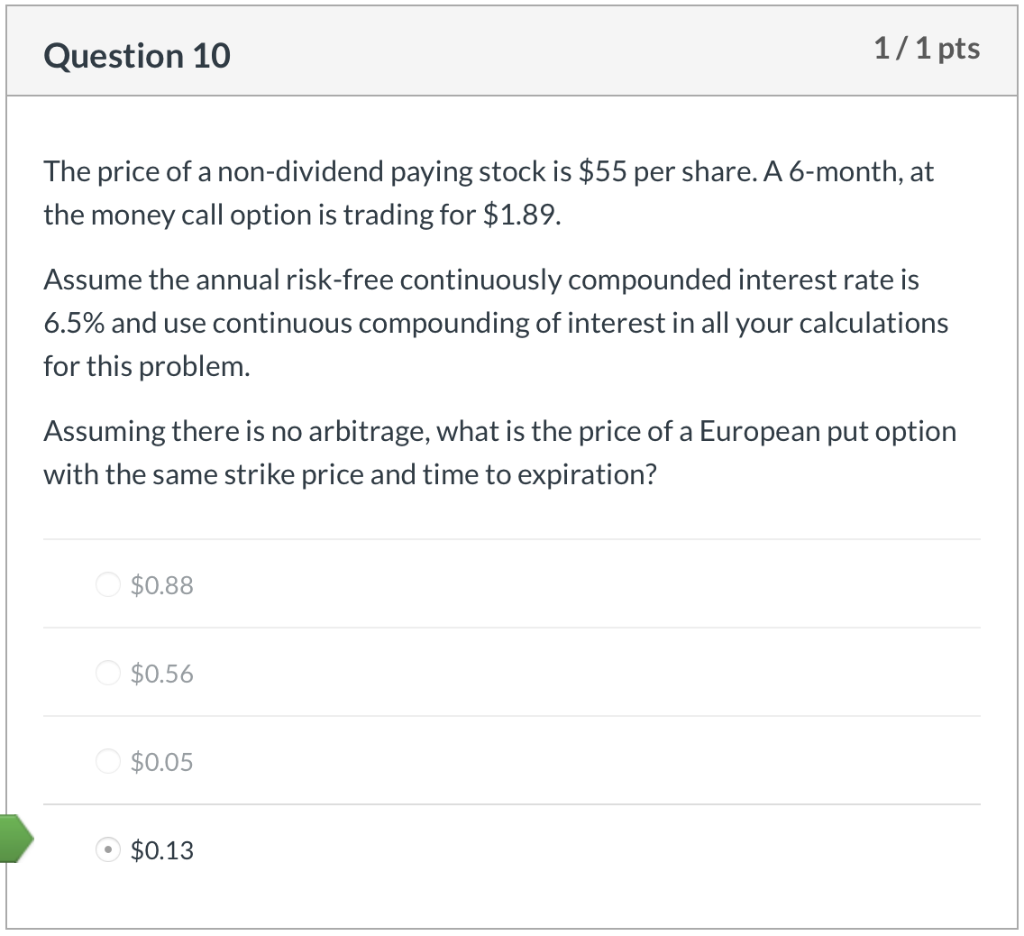
Question 1 1/1 pts Jafee Corp. common stock is priced at $36.50 per share. The company just paid its $0.50 quarterly dividend. The continuously compounded risk free annual interest rate is 6.0%. A $35.00 strike European call, maturing in 6 months, sells for $3.20. What is the price of a 6-month, $35.00 strike put option? O $1.64 $2.38 $2.04 $1.20 Question 2 1/ 1 pts Rankin Corp. common stock is priced at $74.20 per share. The company just paid its $1.10 quarterly dividend. The continuously compounded risk free annual interest rate is 6.0%. A European call option on Rankin Corp. with a strike price of $70.00, maturing in 6 months, sells for $6.50. How much arbitrage profit/loss is made by shorting a $70.00 strike price European put option on Rankin Corp., which is priced at $2.50? $0.12 loss $0.36 loss $0.36 gain O $0.12 gain Question 3 1/1 pts The price of a stock is $52.00. What is the price difference between an at- the-money call option and an at-the-money put option on this stock? Assume 38 days to expiration, a 6.0% annual continuously compounded risk free interest rate, and use continuous compounding of interest in all your calculations for this problem. $0.16 O $0.32 $0.48 $0.64 Question 4 1/1 pts You are given the following: The current price to buy one share of XYZ stock is 500. The stock does not pay dividends. The annual continuously compounded risk-free interest rate is 6%. A European call option on one share of XYZ stock with a strike price of K that expires in one year costs 66.59. A European put option on one share of XYZ stock with a strike price of K that expires in one year costs 18.64. Using put-call parity, calculate the strike price, K. 582 449 559 O 480 452 Question 5 1/1 pts The PS index has the following characteristics: One share of the PS index currently sells for 1,000. The PS index does not pay dividends. Sam wants to lock in the ability to buy this index in one year for a price of 1,025. He can do this by buying or selling European put and call options with a strike price of 1,025. The continuously compounded risk free annual interest rate is 5.0%. Determine which of the following gives the strategy that will achieve Sam's objective and also gives the cost today of establishing this position. Buy the put and sell the call, no cost Buy the put and sell the call, receive 24.99 Buy the call and sell the put, receive 24.99 Buy the call and sell the put, spend 24.99 Buy the put and sell the call, spend 24.99 Question 6 1/1 pts Stock XYZ has the following characteristics: The current price is 40. The price of a 35-strike 1-year European call option is 9.12 The price of a 40-strike 1-year European call option is 6.22 The price of a 45-strike 1-year European call option is 4.08 The annual risk-free interest rate is 8%. Use simple compounding of interest to compute the future value of option premiums when computing profits in this problem. Let S be the price of the stock one year from now. All call positions being compared are long. Determine the range for S such that the 45-strike call produces a higher profit than the 40-strike call, but a lower profit than the 35-strike call. 38.13 42.31 Question 7 1/1 pts Consider a European put option on a stock index without dividends, with 6 months to expiration and a strike price of 1,000. Suppose that the six-month risk-free interest rate is 2%, and that the put costs 74.20 today. Use simple compounding of interest to compute the future value of option premiums when computing profits in this problem. Calculate the price that the index must be in 6 months so that being long the put option would produce the same profit as being short the put option. 924.32 922.83 1,075.68 1,000.00 1,077.17 Question 8 1/1 pts A trader shorts one share of a stock index for 50 and buys a 60-strike European call option on that stock index that expires in 2 years for 10. Assume the annual risk-free continuously compounded interest rate is 3% and use continuous compounding of interest in all your calculations for this problem. Assume that the continuously compounded interest rate you earn on the short sale proceeds, the short rebate rate, is equal to the risk-free rate. The stock index increases to 75 after 2 years. Calculate the profit on your combined position. -22.64 +22.64 +17.53 0 -17.53 Question 9 1/1 pts Jillo, Inc. stock is selling for $54.70 per share. Calls and puts with a $55 strike and 40 days until expiration are selling for $1.65 and $1.23, respectively. Assume the annual risk-free continuously compounded interest rate is 10% and use continuous compounding of interest in all your calculations for this problem. What potential arbitrage profit exists? $0.36 $0.24 $0.12 O$0.48 Question 10 1/1 pts The price of a non-dividend paying stock is $55 per share. A 6-month, at the money call option is trading for $1.89. Assume the annual risk-free continuously compounded interest rate is 6.5% and use continuous compounding of interest in all your calculations for this problem. Assuming there is no arbitrage, what is the price of a European put option with the same strike price and time to expiration? $0.88 $0.56 $0.05 $0.13 Question 1 1/1 pts Jafee Corp. common stock is priced at $36.50 per share. The company just paid its $0.50 quarterly dividend. The continuously compounded risk free annual interest rate is 6.0%. A $35.00 strike European call, maturing in 6 months, sells for $3.20. What is the price of a 6-month, $35.00 strike put option? O $1.64 $2.38 $2.04 $1.20 Question 2 1/ 1 pts Rankin Corp. common stock is priced at $74.20 per share. The company just paid its $1.10 quarterly dividend. The continuously compounded risk free annual interest rate is 6.0%. A European call option on Rankin Corp. with a strike price of $70.00, maturing in 6 months, sells for $6.50. How much arbitrage profit/loss is made by shorting a $70.00 strike price European put option on Rankin Corp., which is priced at $2.50? $0.12 loss $0.36 loss $0.36 gain O $0.12 gain Question 3 1/1 pts The price of a stock is $52.00. What is the price difference between an at- the-money call option and an at-the-money put option on this stock? Assume 38 days to expiration, a 6.0% annual continuously compounded risk free interest rate, and use continuous compounding of interest in all your calculations for this problem. $0.16 O $0.32 $0.48 $0.64 Question 4 1/1 pts You are given the following: The current price to buy one share of XYZ stock is 500. The stock does not pay dividends. The annual continuously compounded risk-free interest rate is 6%. A European call option on one share of XYZ stock with a strike price of K that expires in one year costs 66.59. A European put option on one share of XYZ stock with a strike price of K that expires in one year costs 18.64. Using put-call parity, calculate the strike price, K. 582 449 559 O 480 452 Question 5 1/1 pts The PS index has the following characteristics: One share of the PS index currently sells for 1,000. The PS index does not pay dividends. Sam wants to lock in the ability to buy this index in one year for a price of 1,025. He can do this by buying or selling European put and call options with a strike price of 1,025. The continuously compounded risk free annual interest rate is 5.0%. Determine which of the following gives the strategy that will achieve Sam's objective and also gives the cost today of establishing this position. Buy the put and sell the call, no cost Buy the put and sell the call, receive 24.99 Buy the call and sell the put, receive 24.99 Buy the call and sell the put, spend 24.99 Buy the put and sell the call, spend 24.99 Question 6 1/1 pts Stock XYZ has the following characteristics: The current price is 40. The price of a 35-strike 1-year European call option is 9.12 The price of a 40-strike 1-year European call option is 6.22 The price of a 45-strike 1-year European call option is 4.08 The annual risk-free interest rate is 8%. Use simple compounding of interest to compute the future value of option premiums when computing profits in this problem. Let S be the price of the stock one year from now. All call positions being compared are long. Determine the range for S such that the 45-strike call produces a higher profit than the 40-strike call, but a lower profit than the 35-strike call. 38.13 42.31 Question 7 1/1 pts Consider a European put option on a stock index without dividends, with 6 months to expiration and a strike price of 1,000. Suppose that the six-month risk-free interest rate is 2%, and that the put costs 74.20 today. Use simple compounding of interest to compute the future value of option premiums when computing profits in this problem. Calculate the price that the index must be in 6 months so that being long the put option would produce the same profit as being short the put option. 924.32 922.83 1,075.68 1,000.00 1,077.17 Question 8 1/1 pts A trader shorts one share of a stock index for 50 and buys a 60-strike European call option on that stock index that expires in 2 years for 10. Assume the annual risk-free continuously compounded interest rate is 3% and use continuous compounding of interest in all your calculations for this problem. Assume that the continuously compounded interest rate you earn on the short sale proceeds, the short rebate rate, is equal to the risk-free rate. The stock index increases to 75 after 2 years. Calculate the profit on your combined position. -22.64 +22.64 +17.53 0 -17.53 Question 9 1/1 pts Jillo, Inc. stock is selling for $54.70 per share. Calls and puts with a $55 strike and 40 days until expiration are selling for $1.65 and $1.23, respectively. Assume the annual risk-free continuously compounded interest rate is 10% and use continuous compounding of interest in all your calculations for this problem. What potential arbitrage profit exists? $0.36 $0.24 $0.12 O$0.48 Question 10 1/1 pts The price of a non-dividend paying stock is $55 per share. A 6-month, at the money call option is trading for $1.89. Assume the annual risk-free continuously compounded interest rate is 6.5% and use continuous compounding of interest in all your calculations for this problem. Assuming there is no arbitrage, what is the price of a European put option with the same strike price and time to expiration? $0.88 $0.56 $0.05 $0.13